Guest


Новичок
|
     
Помогите разложить на множители x-y-3x2(2-знак степени)+ 3y2(2-знак степени)Если можно объясните
|
Всего сообщений: Нет | Присоединился: Never | Отправлено: 20 апр. 2007 15:43 | IP
|
|
Silvers


Начинающий
|
     
x - y - 3x^2 + 3y^2 = (x - y) - 3*(x^2 - y^2) = (x - y) - 3*(x - y)*(x + y) = (x - y)*(1 - 3*(x + y))
Использованы аксиомы:
a*x + a*y = a*(x + y)
x + y + z = (x + y) + z = x + (y + z) = y + (x + z)
и очевидное следствие
(x + y)*(x - y) = x^2 - y^2
|
Всего сообщений: 89 | Присоединился: март 2007 | Отправлено: 21 апр. 2007 0:10 | IP
|
|
dantes


Новичок
|
        
Помогите пожалуйста найти коэффициенты многочлена:

В первых четырех можно просто раскрыть скобки, но может есть более простой способ?
|
Всего сообщений: 29 | Присоединился: май 2007 | Отправлено: 14 окт. 2007 14:24 | IP
|
|
Roman Osipov 


Долгожитель
|
         
В первых трех так и поступайте, применение дополнительной теории в них только утяжелит решение.
Что касается четвертого, то я думаю, что эта запись означает следующее:
(x-2)(x-1)(x-0)(x+1)(x+2) (если произведение находится по всем целым j, модуль которых не больше 2)
В пятом примените формулы Виета, выражающие коэффициенты многочлена через его корни.
|
Всего сообщений: 2356 | Присоединился: май 2007 | Отправлено: 14 окт. 2007 15:13 | IP
|
|
dantes


Новичок
|
        
Спасибо. Все получилось.
|
Всего сообщений: 29 | Присоединился: май 2007 | Отправлено: 14 окт. 2007 16:50 | IP
|
|
dantes


Новичок
|
        
Вот еще задачи. С помощью схемы Горнера разложить a(x) по степеням b(x):

Можно конечно просто раскрыть скобки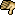 , но при чем тут тогда схема Горнера? , но при чем тут тогда схема Горнера?
И вторая задача. Найти остаток от деления 
на b(x)=x^2-1.
|
Всего сообщений: 29 | Присоединился: май 2007 | Отправлено: 14 окт. 2007 21:33 | IP
|
|
dantes


Новичок
|
        
Помогите пожалуйста.
Выяснить неприводимость многочлена x^8-x^6+x^4-x^2+1 над Q. Можно сделать методом Кронекера, но может есть более простой способ?
|
Всего сообщений: 29 | Присоединился: май 2007 | Отправлено: 25 нояб. 2007 19:28 | IP
|
|
dantes


Новичок
|
        
Пожалуйста помогите кто-нибудь.
|
Всего сообщений: 29 | Присоединился: май 2007 | Отправлено: 5 дек. 2007 8:43 | IP
|
|
Roman Osipov 


Долгожитель
|
         
Не буду мудрствовать, это симметрическое уравнение восьмой степени, его легко решить;

Легко видеть, что все корни комплексные, это означает, что наш полином x^8-x^6+x^4-x^2+1 не приводим над полем Q
|
Всего сообщений: 2356 | Присоединился: май 2007 | Отправлено: 5 дек. 2007 15:16 | IP
|
|
Lyuda

Начинающий
|
       
сорри... для общего развития вопрос - как получилось уравнение t^2-t-1=0 ?
опс... не... понятно все конечно..
(Сообщение отредактировал Lyuda 5 дек. 2007 16:28)
|
Всего сообщений: 73 | Присоединился: ноябрь 2007 | Отправлено: 5 дек. 2007 16:25 | IP
|
|

 Форум
Форум

 Математика
Математика

 Многочлены
Многочлены

 Форум
Форум

 Математика
Математика

 Многочлены
Многочлены