pimpala

Новичок
|
     
Проверьте, пожалуйста, правильно у меня составлена математическая модель задачи?
В производстве пользующихся спросом двух изделий А и Б принимают участие 3 цеха. На изготовление одного изделия А первый цех затрачивает 5 часов, второй цех затрачивает 6 часов, третий - 7 часов. На изготовление одного изделия Б первый цех затрачивает 7 часов, второй - 6, а третий 1 час. На производство всех двух изделий первый цех может затратить не более 256 часов, второй - 283, третий - 363 часов. От реализации одного изделия А фирма получает доход 9р. от изделия Б - 7р. Определить максимальный доход от реализации всех изделий А и Б.
получается такая система ограничений:
5x1+7x2=<256
6x1+6x2=<283
7x1+x2=<363
х1, х2 принадлежат N (множеству натуральных чисел)
целевая функция:
z=9x1+7x2->max
|
Всего сообщений: 2 | Присоединился: апрель 2012 | Отправлено: 27 апр. 2012 0:58 | IP
|
|
MEHT


Долгожитель
|
     
Думаю что нет.
По выпуску изделия "А":
первый цех работает со скоростью v1(А) = 1/5 изделий в час,
второй цех - со скоростью v2(А) = 1/6 изделий в час,
третий цех - со скоростью v3(А) = 1/7 изделий в час;
по выпуску изделия "В":
первый цех работает со скоростью v1(Б) = 1/7 изделий в час,
второй цех - со скоростью v2(Б) = 1/6 изделий в час,
третий цех - со скоростью v3(Б) = 1 изделий в час.
На производство всех двух изделий первый цех может затратить не более 256 часов, второй - 283, третий - 363 часов.
То есть если обозначить через
tn(А) и tn(Б) , где n=1,2,3
времена (в часах), которые затрачивает n-ый цех для изготовления деталей "A" и "Б", то непосредственно из условия можно выписать следующую систему неравенств для этих времён:
t1(А) + t1(Б) ≤ 256,
t2(А) + t2(Б) ≤ 283,
t3(А) + t3(Б) ≤ 363.
Количество деталей A будет суммой от произведений времён на скорости выпуска
n(А) = v1(А) · t1(А) + v2(А) · t2(А) + v3(А) · t3(А),
но тут есть один момент. Количество деталей - число целое. Дробный остаток от каждого слагаемого тут следует выбросить, чтоб слагались целые количества деталей. Именно ОТ КАЖДОГО СЛАГАЕМОГО, в противном случае может случится так, что "недоделка" детали "А" с одного цеха в сумме с "недоделкой" другого даст цельную деталь, что абсурдно. Поэтому правильно будет переписать так:
n(А) = [ v1(А) · t1(А) ] + [ v2(А) · t2(А) ] + [ v3(А) · t3(А) ],
Квадратные скобки обозначают целую часть числа.
Для количества деталей "B" такая же формула
n(Б) = [ v1(Б) · t1(Б) ] + [ v2(Б) · t2(Б) ] + [ v3(Б) · t3(Б) ] .
Очевидно прибыль будет суммой произведений цен на количества
z = a · n(А) + b · n(Б) ,
тут a = 9 и b = 7 - цены, z - прибыль.
Это не всё. Использовать времена, при которых деталь будет недоделана цехом нецелесообразно. В любом случае "квадратные скобки" в формуле для количества деталей уничтожат все нецелые дробные остатки. Поэтому, чтобы избавится от квадратных скобок в соотношениях для количеств деталей будем рассматривать только такие времена, которые кратны обратным "скоростям". То есть положим
t1(А) = (v1(А))-1 · x1(А) ,
t2(А) = (v2(А))-1 · x2(А) ,
t3(А) = (v3(А))-1 · x3(А) ,
t1(Б) = (v1(Б))-1 · x1(Б) ,
t2(Б) = (v2(Б))-1 · x2(Б) ,
t3(Б) = (v3(Б))-1 · x3(Б) ,
где x1(А) , x2(А) , ... , x3(Б) - натуральные числа.
Неравенства и "целевая фунция" представятся тогда так
(v1(А))-1 · x1(А) + (v1(Б))-1 · x1(Б) ≤ 256,
(v2(А))-1 · x2(А) + (v2(Б))-1 · x2(Б) ≤ 283,
(v3(А))-1 · x3(А) + (v3(Б))-1 · x3(Б) ≤ 363,
z = a · (x1(А) + x2(А) + x3(А)) + b · (x1(Б) + x2(Б) + x3(Б)).
Зависимость получилась не от двух, а от шести натуральных чисел.
---
Я не слишком длинно всё расписал?)
Наверное проще воспользоваться готовыми соотношениями из теории оптимизации, чем идти окольными путями. Но увы, я не математик 
(Сообщение отредактировал MEHT 27 апр. 2012 22:03)
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 27 апр. 2012 21:58 | IP
|
|
MEHT


Долгожитель
|
     
Цитата: maxara написал 18 янв. 2012 12:44
Найти кривую y(x) в области гладких функций C1 (первая производная непрерывна),
проходящую через n заданных точек (X1,Y1),(X2,Y2),...,(Xn,Yn)
где a<Xj<b на плоскости XOY и доставляющую минимум функционалу
I=(integral от a до b) F(x,y(x),y'(x))dx
Кто сталкивался с такой задачей поделитесь плиз способами решениями,
ссылками на литературу или идеями?
Пост давний, возможно уже не актуально.. но всё-таки хочется отписаться.
Для каждого интервала
(X1,Y1),(X2,Y2);
(X2,Y2),(X3,Y3);
...
(Xn-1,Yn-1),(Xn,Yn)
это будет (n-1) вариационная задача на минимум функционала
I=(integral от a до b) F(x,y(x),y'(x))dx.
ЭТо стандартная вариационная задача.
Функции y=y(x) каждой из таких задач будут удовлетворять уравнению Лагранжа
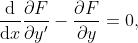
каждая - со своими краевыми условиями.
Вот насчёт гладкости всей кривой - не уверен. Разве что она будет кусочно-гладкой.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 27 апр. 2012 22:13 | IP
|
|
antoniodmir

Новичок
|
     
Всем привет!
Ищу энтузиастов, которые помогут выбрать правильный подход и решить задачу по наиболее эффективному распределению ресурсов для достижения максимального результата. Кто заинтересуется - подробности в ветке "работа", а сюда выкладываю саму задачку.
Мы заняты созданием системы управления контекстной рекламой, которая покупает посетителей в зависимости от их действий на сайте. Для решения основной задачи подходит линейное программирование, но возможно применима и теория нейронных сетей. Будет здорово, если найдется математик, которому будет интересна эта задачка:)
Для начала, небольшое описание системы, ниже постановка задачи.
Общая задача системы.
В рамках бюджета привести максимальное число "эффективных" посетителей на сайт. Под эффективными мы понимаем посетителей, которые выполнили на сайте одно или несколько целевых действий (кликнули на определенную ссылку, просмотрели определенные страницы). Само посещение сайта так же может являться целевым действием.
Время
Цели ставятся на период, кратный одной неделе. Текущая статистика обновляется каждую минуту.
Откуда приходят посетители
С различных сайтов, на которых размещены платные объявления.
На других сайтах размещены рекламные объявления, по которым посетители переходят на наш сайт. В общем случае, количество переходов по каждому объявлению зависит от установленной нами стоимости показа (перехода) Чем выше стоимость, тем больше посетителей видят объявление и переходят по нему.
Помимо объявлений, посетители приходят на наш сайт и самостоятельно (сами набирают адрес или находят нас в поисковых системах). Мы не управляем этими посетителями, но можем прогнозировать посещаемость из этих источников на основе анализа трендов.
Чем управляет система
Система управляет ставками.
В систему загружены все текущие объявления с историей показов и переходов. Число объявлений – от нескольких сотен до сотен тысяч. Система управляет ставкой (стоимостью) объявлений и фактом их показа (при нулевой ставке объявление перестает показываться).
На разных площадках период изменения ставки меняется от 1 часа до 1 суток. Большинство объявлений работают на выполнение одной или нескольких целей, но не всего набора целей. Системе заранее неизвестно, какое объявление вызывает выполнение той или иной цели. Управляя ставками, система добивается выполнения заданного количества целей по минимальной стоимости.
Механизм управления целями. Вводные данные и ограничения.
Система работает в следующих ограничениях:
Максимально эффективно потратить бюджет в заданном отрезке времени (неделя).
Задачи для алгоритмизации
Обнаружение трендов
Каждое объявление имеет свою вероятность выполнения цели на сайте. У одних объявлений она выше, у других ниже. Вероятность плавно меняется во времени (несколько процентов в неделю, в периоды резких взлетов и падений - десятки процентов) по независящим от нас внешним причинам (сезонность спроса, реклама в оффлайне). Эти тренды необходимо выявлять и учитывать при прогнозировании на ближайший период.
Оптимизация затрат (основная задача)
Каждое объявление имеет максимальный и минимальный объем аудитории, который определяется максимальной и минимальной ставкой. Вероятность выполнения целей так же зависит от ставки. Часто, посетители пришедшие по максимальной ставке ведут себя активнее (эмоциональнее), чем пришедшие по минимальной. Необходимо выбрать наиболее эффективный в данный момент набор объявлений. То есть такой, который приведет к выполнению заданного количества каждой цели при минимальной общей стоимости.
Важно учитывать, что выполнение цели имеет вероятностный характер. То есть, даже поставив максимальную ставку самому эффективному объявлению, можно не получить ни одной цели на заданном отрезке времени.
Если вы готовы взяться за эти задачи (кроме них есть еще пара менее существенных), я готов эту работу оплатить.
Работа сдельная (решение нескольких прикладных задач разными методами с последующим тестированием). Оплата 50- 100 тыс., зависит от программистких навыков кандидата.
Для студентов и аспирантов в области линейного программирования проект вполне подойдет на дипломную и пост-дипломную работу.
Возможна удаленная работа с появлением в офисе 1 раз в неделю.
Пишите в личку или телефон-скайп
Антон Иоспа
Деловой Мир Онлайн
+ 7 (903) 176-59-01
skype: a.iospa
|
Всего сообщений: 1 | Присоединился: октябрь 2012 | Отправлено: 10 окт. 2012 19:17 | IP
|
|
Meridian


Новичок
|
      
Прошу помочь с несложной задачей по исследованию операций.
Крис, Джим,Джон и Келли находятся на восточном берегу реки и хотят переправиться на западный берег 7 с помощью каноэ. Каноэ может вместить не более 2 человека. Крис, как наиболее сильный из всех своих друзей, может переправиться через реку за 1 минуту. У Джима, Джона и Келли на это уйдет соответственно 2,5 и 10 минут. Если каноэ находиться 2 человека, то время переправы определяется по слабейшему пассажиру. Цель друзей заключается в переправе на западный берег реки по возможности за минимальное время.
1.Найти не менее двух возможных схем переправы через реку.
2.Определить критерий оценки альтернатив.
3.Какое минимальное время переправы через реку всех друзей?
Если не ошибаюсь, получается 17 (сначала Крис с Джимом плывут, затем Джим возвращается, плывут Джон и Келли, и затем Крис возвращается за Джимом, итого 2+2+10+1+2=17) но ответ я получил методом подбора.
Как корректно решить задачу? Как доказать, что именно это решение -- оптимум?
|
Всего сообщений: 1 | Присоединился: октябрь 2012 | Отправлено: 20 окт. 2012 19:39 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.10.6 Методы оптимизации
2.10.6 Методы оптимизации

 Форум
Форум

 Математика
Математика

 2.10.6 Методы оптимизации
2.10.6 Методы оптимизации