Задачи на вращательное движение тела
(Физика → Теоретическая механика → Основные теоремы динамики → Задача 240)
Условие задачи
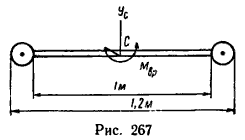
Стержень длиной l=1 м и массой 3 кг имеет на концах шарообразные массы по 2 кг каждая (диаметры шариков d=10 см). Какой вращающий момент нужно приложить к стержню, чтобы привести его во вращение с угловым ускорением ε=2 рад/сек2 вокруг оси, перпендикулярной к стержню и проходящей через центр тяжести системы (рис. 267)?