Теорема Вариньона
(Физика → Теоретическая механика → Произвольная плоская система сил → Задача 68)
Условие задачи
Балансир AB, на который действуют пять горизонтально направленных параллельных сил (рис. 84), должен находиться в равновесии в вертикальном положении, будучи насаженным на горизонтальную ось.
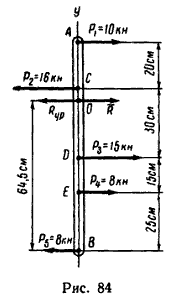
Определить, где необходимо поместить ось балансира, пренебрегая его весом.