Теорема Вариньона
(Физика → Теоретическая механика → Произвольная плоская система сил → Задача 70)
Условие задачи
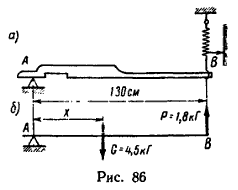
Масса неоднородного стержня составляет 4,5 кг. Для определения положения центра тяжести стержня его левый конец положен на гладкую опору, а правый зацеплен крюком динамометра (рис. 86, а). При горизонтальном положении стержня динамометр показывает усилие 1,8 кГ. Расстояние АВ=130 см от левой опоры до динамометра определено путем непосредственного измерения. Определить положение центра тяжести стержня.