Решение задачи
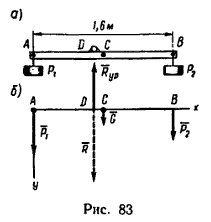
1. Изобразим на рис. 83 в горизонтальном положении планку АВ с грузами Р1=20 н и Р2=15 н. Так как планка однородная, ее вес G=5 н приложен в середине (в точке С).
Таким образом, к планке приложена система трех параллельных сил, действующих в одну сторону (рис. 83, б).
2. Оси проекций расположим, как показано на рис. 83, б.
3. Найдем модуль равнодействующей сил Р1, Р2 и G:
∑ Yi = Р1 + G + Р2 = 20 + 5 + 15 = 40,
R = 40 н.
Равнодействующая направлена вертикально вниз.
4. Определим, на каком расстоянии AD от точки А (левого конца планки) расположена линия действия равнодействующей:
-R * AD = - G * AC - Р2 * AB.
Отсюда
AD= (G*AC + Р2*AB)/R = (5*0,8 + 15*1,6)/40 = 0,7 м.
Линия равнодействующей проходит через точку D на расстоянии 0,7 м от левого конца планки.
В этом месте и необходимо прикрепить к планке петельку. Если теперь за петельку подвесить планку на гвоздь или прикрепить к нити, то планка будет находиться в равновесии, оставаясь горизонтальной, так как равнодействующая R уравновесится реакцией Rур гвоздя или нити.