Теорема Вариньона
(Физика → Теоретическая механика → Произвольная плоская система сил → Задача 66)
Условие задачи
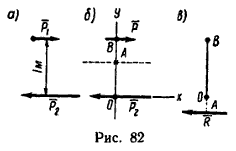
Найти равнодействующую двух параллельных сил Р1 и Р2, направленных в разные стороны, если Р1=12 кн и Р2=60 кн (рис. 82, а).
Теорема Вариньона(Физика → Теоретическая механика → Произвольная плоская система сил → Задача 66) Условие задачиНайти равнодействующую двух параллельных сил Р1 и Р2, направленных в разные стороны, если Р1=12 кн и Р2=60 кн (рис. 82, а).  |
1. Расположим оси Ox и Oy так, как показано на рис. 82, б.
2. Найдем модуль равнодействующей:
∑ Xi = Р1 - Р2 = 12 - 60 = -48.
Следовательно, R = 48 н.
Сумма проекций заданных сил имеет отрицательное значение. Следовательно, равнодействующая направлена влево (ось Ох направлена вправо).
3. Приняв за центр моментов точку O и предположив, что линия действия R пересекает отрезок ОВ в точке A, составим уравнение Вариньона:
R * OA = -Р1 * OB.
Отсюда
OA = -Р1 * OB / R = -12 * 1 / 48 = -0,25 м.
Числовое значение OA получается отрицательным, значит этот отрезок от точки О необходимо отложить в противоположную сторону от ранее предполагаемого.
Равнодействующая заданных сил численно равна 48 н, направлена влево, и линия ее действия лежит ниже точки О на 0,25 м (рис. 82, в).