Теорема Вариньона
(Физика → Теоретическая механика → Произвольная плоская система сил → Задача 65)
Условие задачи
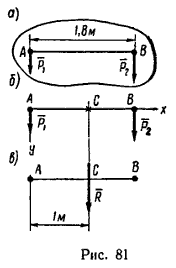
Определить равнодействующую двух параллельных сил Р1 и Р2, направленных в одну сторону (рис. 81, а), если Р1=12 н и Р2=15 н.
Теорема Вариньона(Физика → Теоретическая механика → Произвольная плоская система сил → Задача 65) Условие задачиОпределить равнодействующую двух параллельных сил Р1 и Р2, направленных в одну сторону (рис. 81, а), если Р1=12 н и Р2=15 н.  |
1. Примем за начало осей проекций точку А. Ось х расположим перпендикулярно к данным силам и направим ее вправо, а ось у направим вдоль силы Р1 вниз (рис. 81, б).
2. Найдем модуль равнодействующей:
∑ Yi = Р1 + Р2 = 12 + 15 = 27.
Следовательно, R = 27 н.
Так как сумма проекций положительна, то вектор равнодействующей направлен тоже вниз.
3. Приняв за центр моментов точку А, найдем расстояние АС от точки A до линии действия равнодействующей.
В данном случае
MA(R) = MA(P1) + MA(P2),
но
MA(R) = -R * AC; MA(P1) = 0 и MA(P2) = -P2 * AB,
поэтому
R * AC = P2 * AB.
Откуда
AC = P2 * AB / R = 15 * 1,8 / 27 = 1 м.
Таким образом, равнодействующая двух данных сил численно равна 27 н, и линия ее действия расположена от точки A на расстоянии AC=1 м (рис. 81, в).