Равновесие произвольной плоской системы сил

(Физика → Теоретическая механика → Произвольная плоская система сил → Задача 79)

Условие задачи

На консольную балку, имеющую в точке А шарнирно-неподвижную, а в точке В шарнирно-подвижную опору, действуют две нагрузки (рис. 104, а): в точке D – сосредоточенная нагрузка Р=8 кн, а на участке CB – равномерно распределенная нагрузка интенсивностью q=2 кн/м. Определить реакции опор.

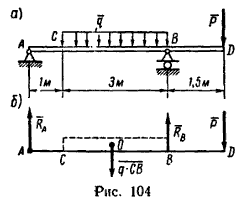
Рис. 104. Консольная балка с шарнирно-неподвижной и шарнирно-подвижной опорами

<< задача 77 || задача 80 >>

Определение реакции опор консольной балки

1. В этой задаче, кроме сосредоточенной силы Р, на участке СВ действует равномерно распределенная сила, интенсивность которой q. Полная величина этой нагрузки (ее равнодействующая) равна q*CB и приложена в точке O посредине участка СВ (рис. 104, б), т.е.
CO = OB = CB/2.

2. Так же как в задаче 75, реакция RB подвижного шарнира направлена вертикально (перпендикулярно к опорной поверхности). Следовательно, и реакция RA неподвижного шарнира направлена вертикально. Таким образом, на балку действует система параллельных сил (см. рис. 104, б).

3. Составим два уравнения моментов относительно точек B и A:
(1) ∑ MB(Pi) = 0; -RA*BA + q*CB*BO - P*BD = 0;
(2) ∑ MA(Pi) = 0; -q*CB*AO + RB*AB - P*AD = 0.

4. Из уравнения (1)
RA = (q*CB*OB - P*BD)/BA = (2*3*1,5 - 8*1,5)/4 = -0,75 кн.

Отрицательное значение реакции RA означает, что она направлена вниз, а не вверх, как показано на рис. 104, б, потому что момент силы Р относительно опоры В больше, чем момент равномерно распределенной нагрузки.

Из уравнения (2) находим RB:
RB = (q*CB*AO - P*AD)/AB = (2*3*2,5 - 8*5,5)/4 = 14,75 кн.

Таким образом, реакция шарнира А равна RA=0,75 кн и направлена вертикально вниз; реакция шарнира В составляет RB=14,25 кн и направлена вертикально вверх.

5. Для проверки решения можно использовать уравнение проекций на вертикальную ось.