Равновесие произвольной плоской системы сил

(Физика → Теоретическая механика → Произвольная плоская система сил → Задача 80)

Условие задачи

На двухконсольную балку с шарнирно-неподвижной опорой в точке A и с шарнирно-подвижной в точке В действуют, как показано на рис. 105, а, сосредоточенная сила Р=10 кн, сосредоточенный момент (пара сил) M=40 кн*м и равномерно распределенная нагрузка интенсивностью q=0,8 кн/м. Определить реакции опор.

<< задача 79 || задача 82 >>

Определение реакции опор двухконсольной балки

Рис. 105. Реакции опор двухконсольной балки

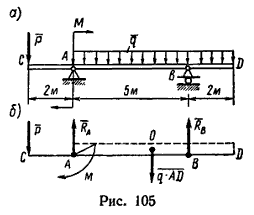
1. В отличие от предыдущей задачи здесь, кроме сосредоточенной силы и равномерно распределенной нагрузки, равнодействующая q*AD которой приложена в точке О посредине участка AD (AO=OD=AD/2=3,5 м), на балку действует момент М, направленный по часовой стрелке (рис. 105, б).

2. После освобождения балки от связей и замены связей их реакциями RA и RB получаем уравновешенную систему, составленную из четырех параллельных сил и одной пары сил (момента).

3. Составим два уравнения моментов относительно точек В и А:
(1) ∑ MB(Pi) = 0; P*BC - RA*BA - M + q*AD*BO = 0;
(2) ∑ MA(Pi) = 0; P*AC - M - q*AD*AO + RB*AB = 0.

4. Решая эти уравнения, находим, что
RA = 7,68 кн и RB = 7,92 кн.