Работа и мощность при поступательном движении

(Физика → Теоретическая механика → Работа и мощность. Коэффициент полезного действия → Задача 225)

Условие задачи

Тело М весом G=50 кГ равномерно перемещается вверх по наклонной плоскости, длина которой l=4 м и угол подъема α=20° (рис. 255, а). Определить работу, производимую силой, направленной параллельно наклонной плоскости, и коэффициент полезного действия наклонной плоскости. Коэффициент трения f=0,2.

<< задача 224 || задача 227 >>

Решение 1

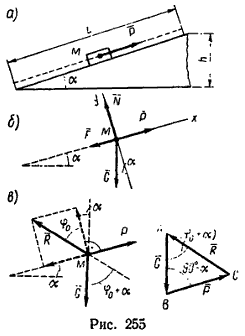
1. При движении тела М (примем его за материальную точку) вверх по наклонной плоскости на него действуют четыре силы: вес G, нормальная реакция наклонной плоскости N, движущая сила Р и сила трения F (рис. 255, б).

Рис. 255. Работа и КПД при перемещении тела вдоль наклонной плоскости

2. Работа силы Р при перемещении тела по длине наклонной плоскости
A = Pl.

3. Найдем необходимую для перемещения тела М силу Р.

Расположив оси координат, как показано на рис. 255, б, составим два уравнения равновесия:
(1) ∑ Xi = 0; P - G sin α - F = 0;
(2) ∑ Yi = 0; N - G cos α = 0.

Дополним эти уравнения третьим уравнением, выражающим основной закон трения:
(3) F = fN.

Из уравнения (1)
P = G sin α + F.

Вместо силы трения F подставим ее значение из уравнения (3):
P = G sin α + fN,
а вместо нормальной реакции N подставим ее значение из уравнения (2):
P = G sin α + fG cos α = G(sin α + f cos α).

4. Следовательно, работа силы P
А = Gl(sin α + f cos α).

После подстановки в это уравнение числовых значений
A = 50*4(sin 20° + 0,2 cos 20°) = 106 кГ*м.

Для перевода в СИ достаточно умножить на ускорение свободного падения g=9,81 м/сек2.

5. Находим к. п. д. наклонной плоскости:
η = Aпол/A.

Полезная работа состоит в подъеме тела весом G на высоту h=l sin 20°, поэтому
η = Aпол/A = (Gl sin 20°)/A = (50*4*sin 20°)/106 = 0,644.

Решение 2

1. Можно считать, что на тело М действуют не четыре, а три силы: G – вес тела, движущая сила Р и полная реакция поверхности реальной связи R, равная геометрической сумме сил N и F (рис. 255, в).

Реакция реальной связи R, как известно (§ 15), при движении отклоняется от нормали к поверхности связи на величину угла трения φ0, причем tg φ0=f, где f – коэффициент трения.

2. Так как на тело М действуют только три силы и они образуют уравновешенную систему (тело М, принятое за материальную точку, движется равномерно и прямолинейно), силовой треугольник ABC, построенный из этих сил, является замкнутым.

3. По рис. 255, в можно определить, что в силовом треугольнике ABC угол B=90°-α, угол A=φ0+α. Следовательно,
∠C = 180° - (∠B + ∠A) = 180° - (90° - α + φ0 + α) = 90° - φ0.

Работа и КПД подъема по наклонной плоскости

Решение 3

1. Известно, что при действии на точку нескольких сил алгебраическая сумма работ всех сил на некотором пути равна работе равнодействующих этих сил (Е. М. Никитин, § 83).

2. В данном случае на тело М, которое примем за материальную точку, действуют четыре силы: вес G, нормальная реакция наклонной плоскости N, сила трения F и движущая сила Р (см. рис 255, б).

3. Точка М движется равномерно и прямолинейно. Равнодействующая сил, действующих на точку, равна нулю, и, следовательно, алгебраическая сумма работ, производимых силами G, N, F и Р на длине l наклонной плоскости, также равна нулю:
AG + AN + AF + AP = 0.

4. Находим отсюда работу силы Р:
(а) AP = -(AG + AN + AF),
где работа силы G
AG = Gl cos (90° + α) = -Gl sin α
работа силы N, направленной перпендикулярно к направлению движения точки, равна нулю:
AN = Nl cos 90° = 0;
работа силы F
AF = Fl cos 180° = -Fl = -fGl cos α,
так как сила трения
F = fN = fG cos α.

Подставим в выражение (а) полученные значения работ:
AP = -(AG + AN + AF) = Gl sin α + fGl cos α.

Таким образом,
A = AP = Gl(sin α + f cos α) = 50*4*(sin 20° + 0,2 cos 20°) = 106 кГ*м.

5. К. п. д. наклонной плоскости найдем так же, как в п. 5 первого решения.