Работа и мощность при поступательном движении(Физика → Теоретическая механика → Работа и мощность. Коэффициент полезного действия → Задача 224) Условие задачиКакую работу необходимо произвести, чтобы равномерно передвинуть в горизонтальном направлении на расстояние s клинчатый ползун 1 вдоль направляющих 2? Вес ползуна G, угол заострения ползуна и направляющих α (рис. 254, а), коэффициент трения между ползуном и направляющими f.  |
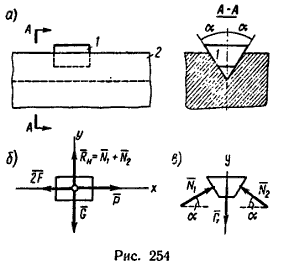
1. На клинчатый ползун, когда он находится в горизонтально расположенных направляющих, действуют три силы: вес ползуна G и две реакции направляющих N1 и N2 (рис. 254, в), действующих на ползун перпендикулярно к боковым плоскостям (щекам) ползуна.
Для приведения ползуна в движение к нему нужно приложить параллельно направляющим силу P и тогда возникнут еще две силы – силы трения, действующие вдоль обеих боковых плоскостей ползуна (см. рис. 254, б – здесь вектор RН изображает направленную вертикально вверх геометрическую сумму нормальных реакций N1 и N2).
Таким образом, на ползун при его движении действуют всего шесть сил: G, N1, N2, F1, F2 и P.
В данном случае нормальные реакции N1 и N2 равны между собой, следовательно, равны и силы трения F1 и F2, поэтому N1=N2=N и F1=F2=F.
2. Работа при перемещении ползуна на расстояние s
A = Ps,
но предварительно найдем числовое значение движущей силы P.
3. Спроектировав приложенные к ползуну силы на ось х (см. рис. 254, б), получим
P = 2F.
Но F=fN, поэтому
(а) P = 2fN.
Нормальную реакцию N найдем из уравнения проекций на ось y (см. рис. 254, в):
2N sin α - G = 0
и
N = G/(2 sin α).
Подставляем найденное значение N в (а):
(б) P = fG/sin α.
4. Следовательно, работа при передвижении клинчатого ползуна на расстояние s
A = Ps = fGs/sin α.
Примечание. Входящая в формулу (б) величина f/sin α называется коэффициентом трения клинчатого ползуна. При уменьшении угла α (при большем заострении ползуна и направляющих) коэффициент трения клинчатого ползуна резко увеличивается.