Решение 1 (с применением метода проекций)
1. Если масса шарика m=2 кг, то его вес G=mg=2*9,81=19,62 н. Кроме веса, на шарик действует натяжение (реакция T) нити. Длина нити l=60 см=0,6 м.
Изобразим двигающийся шарик с приложенными к нему силами G и T (рис. 250, а). Так как шарик движется по окружности равномерно, то он имеет только нормальное ускорение an, направленное по радиусу АО=r окружности. Применяя принцип Даламбера, для уравновешивания сил T и G приложим к шарику нормальную (центробежную) силу инерции Pnи.
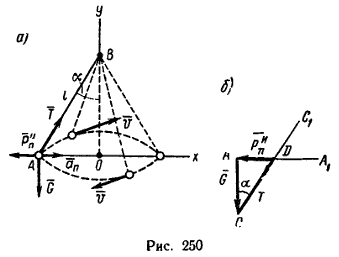
Изображая на рис. 250 силу инерции, необходимо учитывать, что она прикладывается к шарику условно. В действительности, сила инерции, как известно, приложена к двигающему телу или к связи. В данном случае нить служит для шарика и двигающим телом (через нить шарик приводится в движение), и связью (нить одновременно и ограничивает движение шарика). Поэтому сила инерции приложена к нити и отклоняет ее от вертикали.
2. Совместив оси координат с прямыми AO и BO и спроектировав силы на оси х и у, выведем уравнения равновесия:
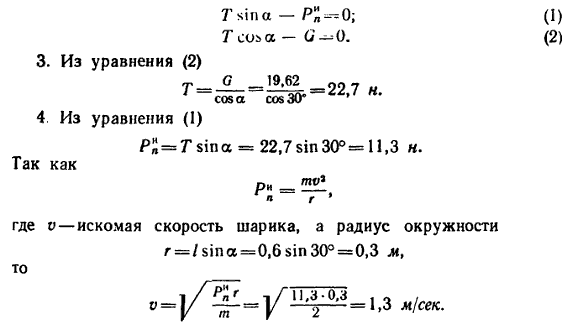
Таким образом, натяжение нити составляет 22,7 н при скорости движения шарика 1,3 м/сек.
Решение 2 (с применением графо-аналитического метода)
