Применение принципа Даламбера к решению задач на криволинейное движение точки

(Физика → Теоретическая механика → Движение материальной точки → Задача 215)

Условие задачи

Шарик, масса которого m=0,5 кг, привязан к нити длиной 0,7 м. Нить вместе с шариком вращается в вертикальной плоскости, затрачивая на один оборот 1 сек. Определить натяжение шнура в моменты высшего и низшего положения шарика, считая, что скорость остается постоянной при перемещении по всей длине окружности.

<< задача 212 || задача 216 >>

Решение задачи

Рис. 249. Натяжение шнура при движении шарика

1. В соответствии с условием задачи считаем, что шарик движется равномерно по окружности, радиус которой равен длине нити (r=0,7 м). Следовательно, его скорость
v = 2πr/T = 2*3,14*0,7/1 ≈ 4,4 м/сек.

Оставаясь численно неизменной, скорость точки непрерывно изменяет направление, значит точка имеет нормальное ускорение
an = v2/r = 4,42/0,7 = 27,6 м/сек2.

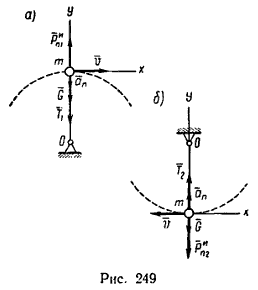
2. Рассмотрим движущийся шарик в тот момент, когда он проходит через верхнюю точку траектории (рис. 249, а).

На шарик действуют две силы: его вес G и реакция нити Т1, равная ее натяжению. Заметим, что обе силы направлены в одну сторону – к точке О подвеса, так как вес всегда направлен вертикально вниз. Реакция гибкой связи всегда направлена вдоль нити от тела, которое удерживается нитью. Шарик, привязанный к нити и приведенный в движение, стремится согласно закону инерции двигаться равномерно и прямолинейно и поэтому он постоянно натягивает нить.

3. Добавим к силам G и Т силу инерции Pn1и, направив ее в сторону, противоположную ускорению an. Образовав таким образом уравновешенную систему сил, получим уравнение равновесия
∑ Yi = 0; Pn1и - G - T1 = 0.

4. Из уравнения разновесия находим T1, учитывая, что Pn1и=man и G=mg:
T1 = Pn1и - G = m(an - g).

Подставим в это уравнение числовые значения:
T1 = 0,5(27,6 - 9,81) = 0,5*17,8 = 8,9 Н.

Таким образом, находясь в верхнем положении, двигающийся шарик натягивает нить силой 8,9 н.

Отметим, что натяжение нити будет ослабевать при уменьшении скорости движения шарика. Следовательно, для того чтобы шарик при движении в вертикальной плоскости смог пройти верхнюю точку траектории с заданным радиусом кривизны R, он должен иметь в этой точке определенную скорость.

5. Рассмотрим теперь движущийся шарик в момент прохождения им нижней точки траектории (рис. 249, б).

В этом положении на шарик действуют также две силы: вec G и реакция нити T2, но в отличие от предыдущего случая эти силы, действуя вдоль одной прямой, направлены в противоположные стороны.

6. Добавим к силам G и T2 силу инерции Pn2и и составим уравнение равновесия:
∑ Yi = 0; T2 - G - Pn2и = 0.

7. Находим T2:
T2 = G + Pn2и = m(g + an) = 0,5(9,81 + 27,6) = 18,7 Н.

Как видно, при прохождении через нижнюю точку траектории шарик создает наибольшее натяжение нити.