Применение принципа Даламбера к решению задач на криволинейное движение точки(Физика → Теоретическая механика → Движение материальной точки → Задача 217) Условие задачиТонкий стержень АВ, центр тяжести которого расположен на его оси O, вращается с угловой скоростью n=3000 об/мин. На сколько увеличится нагрузка на подшипник, в котором вращается стержень, если на одну из половинок стержня прикрепить массу m=0,5 кг, на расстоянии R=0,1 м от оси вращения (рис. 251, а).  |
1. Стержень АВ без прикрепленной к нему массы m создает нагрузку на подшипник, равную его собственному весу. Причем, если стержень хорошо центрирован, т. е. его центр тяжести расположен точно на оси подшипника, то нагрузка при вращении не изменится – она также будет равна весу стержня и будет действовать на подшипник вертикально вниз.
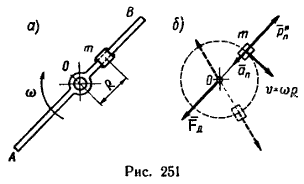
2. Если к стержню, по условию задачи, прикрепить массу m, то эта масса (примем ее за материальную точку), двигаясь по окружности радиусом R=0,1 м начнет растягивать ту часть стержня, которая расположена между массой m и подшипником, силой, равной Pnи. Благодаря этому возникает дополнительная так называемая динамическая нагрузка на подшипник, уравновешиваемая его реакцией Fд (рис. 251, б).
3. Так как увеличение нагрузки равно возникшей силе инерции Pnи, то и определим эту силу по формуле (3):
Pnи = mω2R,
где
m = 0,5 кг, R = 0,1 м и ω = πn/30 = 3,14*3000/30 = 314 рад/сек.
Подставим эти значения в формулу (3):
Pnи = 0,5*3142*0,1 = 4929,8 Н ≈ 4,93 кН.
Таким образом, в результате прикрепления массы m нагрузка на подшипник увеличивается почти на 5 кН.
Результат, получившийся в этой задаче, подтверждает необходимость тщательной балансировки вращающихся деталей машин. Несбалансированные детали при вращении создают огромные дополнительные динамические нагрузки, которые приводят к быстрому износу подшипников.