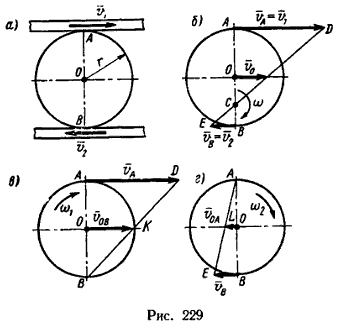
Решение 1 (при помощи мгновенного центра скоростей)
1. В данном случае известны скорости реек. Но так как диск катится между ними без скольжения, точки A и B в местах соприкосновения диска с рейками имеют те же скорости . Следовательно, vA=v1 и vB=v2 (рис. 229, б). Как видно, точки А и В лежат на прямой, перпендикулярной к направлениям этих скоростей. Соединив концы D и Е векторов AD и BE, изображающих скорости vA и vB, найдем на прямой АВ точку С – мгновенный центр скоростей диска (Е. М. Никитин, § 72).
2. Скорость v0 центра диска определяется по формуле
v0 = ω*OC,
где ω – угловая скорость диска.
3. Величины угловой скорости ω и расстояния ОС находим из равенств:
ω = vA/AC = vA/(r + OC) и ω = vB/BC = vB/(r - OC).
Так как левые части обоих равенств равны между собой, то
vA/(r + OC) и ω = vB/(r - OC),
отсюда
OC = r(vA - vB)/(vA + vB) = 0,5(8 - 2)/(8 + 2) = 0,3 м
и
ω = vA/(r + OC) = 8/(0,5 + 0,3) = 8/0,8 = 10 рад/сек.
4. Находим скорость v0:
v0 = ω*OC = 10*0,3 = 3 м/сек.
Решение 2 (методом последовательной остановки реек)
1. Плоское движение диска образуется вследствие независимого друг от друга перемещения реек. Поэтому скорость центра диска можно получить как результат геометрического сложения скоростей, получаемых точкой O от перемещения каждой рейки.
2. Мысленно остановим нижнюю рейку (рис. 229, в). Тогда благодаря передвижению верхней рейки диск будет катиться по нижней без скольжения и в точке В образуется мгновенный центр скоростей.
Соединим точку В с точкой D (концом вектора vA) и получим треугольник BAD, в котором вектор ОК=vOB изображает скорость центра диска при неподвижной нижней рейке.
Так как ОК – средняя линия треугольника BAD,
vOB = vA/2 = 8/2 = 4 м/сек.
Угловая скорость диска в этом движении
ω1 = vA/AB = 8/1 = 8 рад/сек.
3. Теперь мысленно остановим верхнюю рейку (рис. 229, г). Диск будет катиться без скольжения по верхней рейке, имея мгновенный центр скоростей в точке А.
Соединив точку А с концом Е вектора vB, получим треугольник ABE, определяющий скорость vOA=OL центра диска при неподвижной верхней рейке.
И здесь OL – средняя линия треугольника ABE, поэтому
vOA = vB/2 = 2/2 = 1 м/сек.
Угловая скорость диска в этом движении
ω2 = vB/BA = 2/1 = 2 рад/сек.
4. При одновременном движении обеих реек скорость центра диска
v0 = vOA - vOB = 4 - 1 = 3 м/сек,
так как обе скорости vOA и vOB направлены вдоль одной прямой, но в противоположные стороны.
5. Угловая скорость диска определяется как сумма угловых скоростей ω1 и ω2, найденных выше:
ω = ω1 + ω2 = 8 + 2 = 10 рад/сек.