Определение положения центра тяжести фигур, составленных из пластинок

Решение задачи

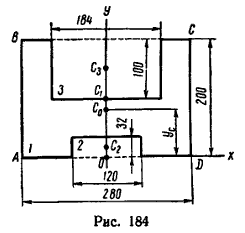
1. Пластинка имеет ось симметрии, на которой находится центр тяжести. Совместим с осью симметрии ось у, а ось x – с нижним краем пластинки.

2. Дополнив пластинку до прямоугольника ABCD, разобьем ее тем самым на три части: 1, 2 и 3.

3. Определим площади каждой части в см² и координаты их центров тяжести в см:
F₁ = 28*20 = 560 см²; C₁(0; 10);
F₂ = -12*3,2 = -38,4 см²; C₂(0; 1,6);
F₃ = -18,4*10 = -184 см²; C₃(0; 15).

4. Определим ординату центра тяжести пластинки, подставив найденные значения во вторую формулу системы (3):
y_c = (∑ F_iy_i) / ∑ F_i,
y_c = (560*10-38,4*1,6-184*15)/(560-38,4-184) ≈ 8,23 см.

Таким образом, центр тяжести С₀ имеет ординату y_c ≈ 82 мм.