Определение положения центра тяжести фигур, составленных из пластинок

(Физика → Теоретическая механика → Центр тяжести → Задача 126)

Условие задачи

Определить положение центра тяжести фигуры, составленной из трех тонких плоских пластинок прямоугольной формы, пересекающихся друг с другом под прямыми углами (рис. 182); размеры – в мм.

Рис. 182. Определение центра тяжести фигуры, составленной из пластинок

<< задача 124 || задача 127 >>

Решение задачи

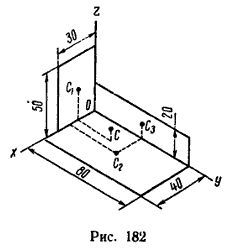
1. Поместим начало координат в вершине трехгранного угла и расположим оси координат вдоль линий пересечения пластинок.

Фигура состоит из трех прямоугольников с центрами тяжести C1, C2, C3, расположенными на пересечении прямых, соединяющих середины противоположных сторон.

2. Исходя из размеров фигуры, определим необходимые данные для подстановки в формулы (3): Fi – площади прямоугольников и координаты xi, yi и zi их центров тяжести:
F1 = 3*5 = 15 см2; C1(1,5; 0; 2,5);
F2 = 4*8 = 32 см2; C2(2; 4; 0);
F3 = 8*2 = 16 см2; C3(0; 4; 1).

3. Подставим эти данные в формулы (3) и вычислим искомые координаты центра тяжести фигуры:
xc = (15*1,5+32*2+16*0)/(15+32+16) = 86,5/63 = 1,37 см = 13,7 мм;
yc = (15*0+32*4+16*4)/(15+32+16) = 192/63 = 3,04 см = 30,4 мм;
zc = (15*2,5+32*0+16*1)/(15+32+16) = 53,5/63 = 0,85 см = 8,5 мм.

Центр тяжести фигуры расположен в точке C(13,7; 30,4; 8,5).