Определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму

Решение задачи

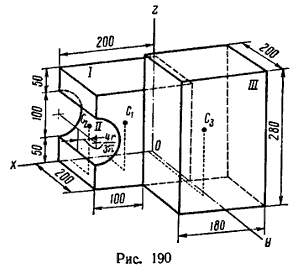
1. Тело состоит из куба I, полуцилиндра II, объем которого считаем отрицательным, так как он вырезан из объема куба I, и прямоугольного параллелепипеда III.

2. Отметив на рисунке положение центра тяжести составных частей (C₁ – центр тяжести куба, C₂ – центр тяжести полуцилиндра и C₃ – центр тяжести параллелепипеда), найдем исходные величины для подстановки их в формулы (4) – объемы V_i и координаты x_i, y_i, z_i их центров тяжести:
V₁ = 8000 см³; C₁(10; 10; 10);
V₂ = -785 см³; C₂(17,9; 10; 10);
V₃ = 10080 см³; C₃(1; 30; 14).

3. После подстановки в расчетные формулы имеем:
x_c = (8000*10-785*17,9+10080*1)/(8000-785+10080) ≈ 4,40 см ≈ 44 мм;
y_c = (8000*10-785*10+10080*30)/(8000-785+10080) ≈ 21,6 см ≈ 216 мм;
z_c = (8000*10-785*10+10080*14)/(8000-785+10080) ≈ 10,6 см ≈ 106 мм.

Таким образом, центр тяжести данного тела находится в точке С₀(44; 216; 106).