Равномерное прямолинейное движение точки

(Физика → Теоретическая механика → Кинематика точки → Задача 135)

Условие задачи

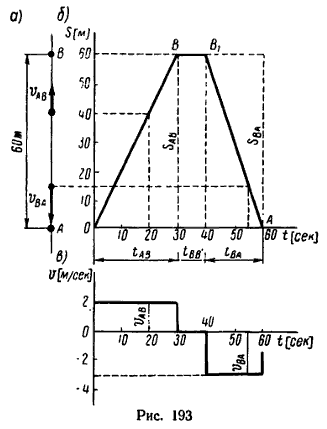
Точка, совершая равномерное и прямолинейное движение, проходит прямолинейный участок траектории АВ, равный 60 м (рис. 193, а) за 30 сек. Простояв затем 10 сек на месте, точка возвращается в исходное положение со скоростью 3 м/сек. Сколько всего времени проходит от начала движения точки до ее возвращения в исходное положение? Какой путь проходит точка?

Построить графики перемещения и скорости точки.

Рис. 193. График движения точки

<< задача 133 || задача 136 >>

Решение задачи

1. Расстояние от А до В, равное sAB=60 м, равномерно пройдено за tAB=30 сек. В данном случае начальное расстояние s0=0, поэтому из уравнения (б) находим скорость точки на участке АВ:
vAB = sAB/tAB = 60/30 = 2 м/сек.

2. Точка находится в покое в течение времени tBB'=10 сек.

3. Точка возвращается в исходное положение, пройдя расстояние от В до А sBA=60 м со скоростью vBA=3 м/сек за время
tBA = sBA/vBA = 60/3 = 20 сек.

4. Время от начала движения до момента возвращения в исходное положение равно:
tAB + tBB' + tBA = 30 + 10 + 20= 60 сек = 1 мин.

5. Путь, пройденный точкой за это время,
s = sAB + sBA = 60 + 60 = 120 м.

6. Построим теперь график перемещения (рис. 193, б) и скорости точки (рис. 193, в) с одинаковым масштабом по оси времени.