Roman Osipov 


Долгожитель
|
         
Числовые ряды: теория и конкретные примеры.
Для вопросов сходимости есть соотв. тема!
|
Всего сообщений: 2356 | Присоединился: май 2007 | Отправлено: 19 апр. 2009 14:12 | IP
|
|
Svetik1989


Новичок
|
      

Погомогите решить)))заранее спасибо
(Сообщение отредактировал attention 21 фев. 2010 4:27)
|
Всего сообщений: 16 | Присоединился: ноябрь 2008 | Отправлено: 27 апр. 2009 12:01 | IP
|
|
Sergey91


Новичок
|
     
Помогите решить:
Для данного ряда записать последовательность его частных сумм, затем пользуясь непосредственно определением, доказать сходимость ряда и найти его сумму.
Задания приведены на картинке:

|
Всего сообщений: 14 | Присоединился: май 2009 | Отправлено: 21 мая 2009 20:27 | IP
|
|
Olegmath2

Полноправный участник
|
      
№1. Решение.
Sum{1_+бесконечность}(1/(4n^2-1)).
a_n=1/(4n^2-1)=1/((2n-1)*(2n+1))=A/(2n-1)+B/(2n+1).
Найдём с помощью метода неопределённых коэффициентов неизвестные A и B из равенства:
1/((2n-1)*(2n+1))=A/(2n-1)+B/(2n+1), (*)
Умножим обе части равенства (*) на общий знаменатель всех дробей, фигурирующих в этом равенстве, т.е. на (2n-1)*(2n+1). Тогда получим равенство:
1=A*(2n+1)+B*(2n-1);
1=2An+A+2Bn-B;
1=(2A+2B)*n+(A-B);
0*n+1=(2A+2B)*n+(A-B);
У равных многочленов соответствующие коэффициенты равны. Следовательно,
{2A+2B=0, (1)
{A-B=1, (2)
(1) => 2A=-2B => A=-B, (3) => (2) => -B-B=1; -2B=1; B=-1/2 => (3) => A=1/2.
{A=1/2,
{B=-1/2.
Подставим найденные значения A и B в равенство (*):
a_n=1/((2n-1)*(2n+1))=(1/2)/(2n-1)-(1/2)/(2n+1), (4).
Запишем выражение для n-й частичной суммы данного ряда и преобразуем его, пользуясь равенством (4).
S_n=a_1+a_2+a_3+…+a_(n-1)+a_n=
=1/2*(1/1-1/3+1/3-1/5+1/5-1/7+…+1/(2n-3)-1/(2n-1)+1/(2n-1)-1/(2n+1))=
=1/2*(1/1-1/(2n+1))=1/2-1/(2*(2n+1)) => S_n=1/2-1/(2*(2n+1)).
Теперь найдём сумму S данного ряда, используя определение:
S=lim{n->+бесконечности}(S_n)= lim{n->+бесконечности}(1/2-1/(2*(2n+1)))=1/2.
Ответ: S_n=1/2-1/(2*(2n+1)), S=1/2.
Задача №2 решается аналогичным образом. Для решения задачи №3 воспользуйтесь формулой суммы первых n членов геометрической прогрессии.
|
Всего сообщений: 235 | Присоединился: февраль 2009 | Отправлено: 21 мая 2009 21:47 | IP
|
|
belka 456

Новичок
|
     
Помогите решить

(Сообщение отредактировал attention 21 фев. 2010 4:27)
|
Всего сообщений: 7 | Присоединился: июнь 2009 | Отправлено: 8 июня 2009 16:33 | IP
|
|
Anatoly

Новичок
|
     
Добрый день, помогите с решением, пожалуйста

(Сообщение отредактировал attention 21 фев. 2010 4:28)
|
Всего сообщений: 2 | Присоединился: июнь 2009 | Отправлено: 11 июня 2009 23:56 | IP
|
|
Arhangel1990

Новичок
|
     
Помогите пожалуйста решить:
а)Sum{1_+бесконечность}1-cos(sqrt(n))/n^2+n-1
б)Sum{1_+бесконечность}1*3*5(2n-1)/3^n(n+1)!
в)Sum{1_+бесконечность}(4n-1/3n+2)^n
г)Sum{1_+бесконечность}(-1)^n/n*(n+1)
|
Всего сообщений: 30 | Присоединился: июнь 2009 | Отправлено: 11 окт. 2009 14:34 | IP
|
|
Sav

Новичок
|
     
Помогите решить....взаранее спасибо))))
Найти интервал сходимости степного ряда
Sum{1_+бесконечность}AnX^n
а)2n/n^n
б)1/(n+2)ln(n+2)
|
Всего сообщений: 8 | Присоединился: январь 2009 | Отправлено: 11 окт. 2009 15:00 | IP
|
|
SSSergey


Новичок
|
     
Помогите пожалуйста решить задачки
1

2

|
Всего сообщений: 27 | Присоединился: октябрь 2009 | Отправлено: 21 фев. 2010 1:18 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: SSSergey написал 21 фев. 2010 1:18
Помогите пожалуйста решить задачки
1

2


Найдем радиус 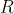 сходимости степенного ряда. сходимости степенного ряда.



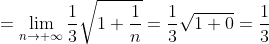
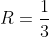

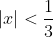
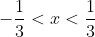
Таким образом, исходный степенной ряд  сходится на интервале сходится на интервале . )
Рассмотрим граничные точки 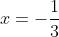 и и 
При 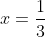 исходный ряд исходный ряд  принимает вид принимает вид 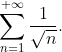 Извесно, что данный ряд является расходящимся. Извесно, что данный ряд является расходящимся.
Таким образом, исходный степенной ряд  при при 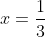 расходится. расходится.
При 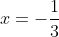 исходный степенной ряд исходный степенной ряд  принимает вид принимает вид ^{n} }{\sqrt{n} }. )
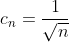
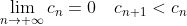
По теореме Лейбница ряд ^{n} }{\sqrt{n} } ) является сходящимся. Таким образом, при является сходящимся. Таким образом, при 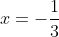 исходный степенной ряд исходный степенной ряд  сходится. сходится.
В итоге, степенной ряд  сходится на полуинтервале сходится на полуинтервале . )
(Сообщение отредактировал RKI 21 фев. 2010 16:05)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 21 фев. 2010 15:55 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.15 Числовые ряды
2.1.15 Числовые ряды

 Форум
Форум

 Математика
Математика

 2.1.15 Числовые ряды
2.1.15 Числовые ряды