attention 


Долгожитель
|
      
Цитата: dokata написал 1 дек. 2009 20:36
Здравствуйте! Помогите, пожалуйста, решить. 
1.Вычислить:
а) sin^2 1 + sin^2 2 + sin^2 3 + ... + sin^2 90
(всё в градусах)
заранее спасибо. )
Во-первых, переведите градусы в радианы и упростите квадрат синуса по известной формуле

Т.е. имеем:

Теперь оценим последнюю сумму: центральный член суммы равен нулю, т.е.
при 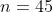 имеем имеем 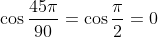 . Так как косинус на интервале . Так как косинус на интервале
) положителен, а на интервале отрицателен положителен, а на интервале отрицателен 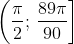 , то, , то,
следовательно, имеем: 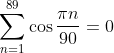 . .
Окончательно
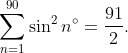
(Сообщение отредактировал attention 2 дек. 2009 19:40)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 2 дек. 2009 20:28 | IP
|
|
dokata

Новичок
|
     
Мы ещё двойной угол в школе не проходили. А я сделала так:
1.нужно разбить на пары(кроме 45 и 90) (всего 44 пары)
2.рассмотреть первую пару.
sin^2 1 + sin^2 89 = sin^2 1 + cos^2 1 = 1.
Сумма других пар будет такой же, значит, теперь можно вычислить сумму:
S = 44 + sin^2 (45) + sin^2 (90) = 45,5
|
Всего сообщений: 11 | Присоединился: январь 2009 | Отправлено: 3 дек. 2009 8:50 | IP
|
|
cvetkir

Новичок
|
      
Помогите, пжалуйста, упростить
3sinα * cos3α + 9sinα – sin3α * cos3α – 3sin3α * sosα
|
Всего сообщений: 1 | Присоединился: ноябрь 2012 | Отправлено: 8 нояб. 2012 20:28 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 1.3 Тождественные преобр. тригонометрических выражений
1.3 Тождественные преобр. тригонометрических выражений

 Форум
Форум

 Математика
Математика

 1.3 Тождественные преобр. тригонометрических выражений
1.3 Тождественные преобр. тригонометрических выражений