Решение задачи
1. В задаче известно время движения заторможенного автомобиля, т. е. имеется в виду импульс силы, поэтому для ее решения применим формулу (1) – закон количества движения.
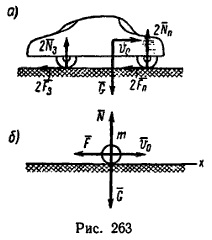
2. На заторможенный автомобиль действуют девять сил (рис. 263, а): G – вес автомобиля, четыре реакции поверхности дороги, приложенные к каждому колесу, и четыре силы трения, также приложенные к колесам.
Принимая автомобиль за материальную точку, считаем, что все эти силы приложены в центре тяжести автомобиля, и тогда, заменив четыре реакции поверхности их суммой N и четыре силы трения их суммой F, получим только три силы G, N и F (рис. 263, б).
3. Силы G и N численно равны друг другу и взаимно уравновешиваются. Следовательно, импульс создается силой трения F.
4. Импульс силы трения в данном случае действует в сторону, противоположную движению, поэтому уравнение (1) для данной задачи примет вид
mv - mv0 = -Ft.
Но автомобиль через t=5 сек останавливается (v=0), поэтому
mv = 0.
Следовательно
-mv0 = -Ft или mv0 = Ft.
5. Подставим сюда значения m=G/g и F=fN=fG (так как N=G):
Gv0/g = fGt.
Откуда, имея в виду, что v0=60 км/ч=16,7 м/сек,
f = v0/(gt) = 16,7/(9,81*5) = 0,34.
Эту задачу можно решить, используя теорему об изменении кинетической энергии. Рекомендуем этот вариант решения выполнить самостоятельно.