Разложение силы на две составляющие

Решение графо-аналитическим методом по правилу параллелограмма

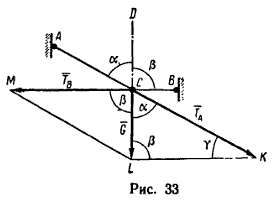
1. Исходя из условия задачи, построим чертеж (рис. 33). Из точки C проводим вертикальный отрезок CL, изображающий вектор G. Отложив (приблизительно) от вертикали CD влево угол α, а вправо – угол β, проведем нити CA и CB (длины нитей не влияют на величину усилий, поэтому точки A и B выбираем произвольно).

2. Вектор G по правилу параллелограмма разложим на две составляющие T_A и T_B, направленные вдоль нитей, т. е. построим параллелограмм CKLM.

3. На основе построения параллелограмма CKLM очень просто определяются его углы:
∠KCL = α = 65°, ∠MCL = ∠CLK = β = 90°
и, следовательно,
∠CKL = γ = 180° - (α + β) = 180° - 155° = 25°.

4. Так как силовой параллелограмм делится на два прямоугольных треугольника, то легко найти оба усилия:
T_A = G/sin γ = 12/sin 25° = 28,4 кГ;
T_B = G/tg γ = 12/tg 25° = 25,7 кГ.

В единицах СИ усилия равны:
T_A = 28,4 кГ * 9,81 н/кГ = 279 н;
T_B = 25,7 кГ * 9,81 н/кГ = 252 н.

Задачи 22, 23 и 24 относятся к первому типу задач на разложение силы по правилу параллелограмма или треугольника (см. § 2).

Рассмотрим теперь по одной задаче второго (задача 25), третьего (задача 26) и четвертого (задача 27) типов.