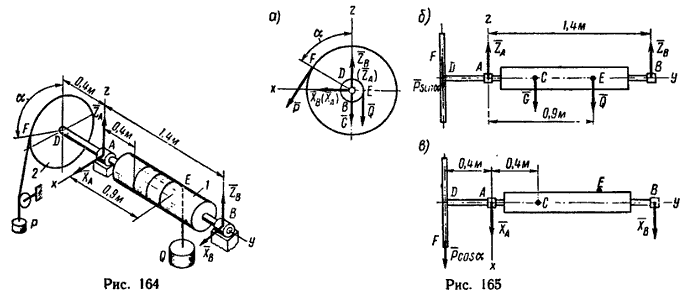
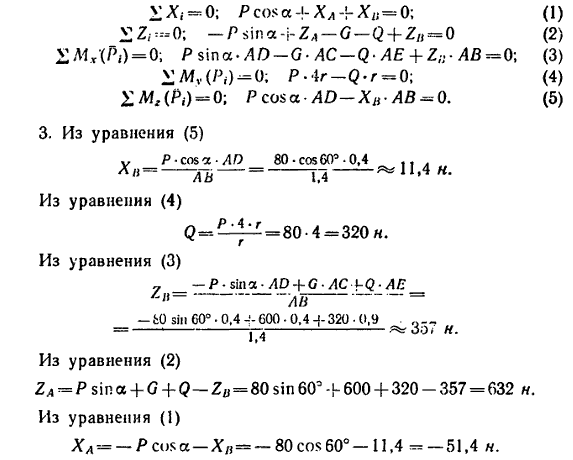Равновесие произвольной пространственной системы сил

(Физика → Теоретическая механика → Пространственная система сил → Задача 116)

Условие задачи

На вал 1 ворота намотана веревка, удерживающая груз Q (рис. 164). Радиус колеса 2 ворота в четыре раза больше радиуса вала. Веревка, прикрепленная к ободу колеса и натягиваемая грузом силой Р=80 н, сходит с колеса в точке F по касательной; радиус DF колеса образует с вертикалью угол α=60°. Определить величину груза Q, при котором ворот остается в равновесии, а также реакции подшипников A и В, если общий вес вала и колеса G=600 н и приложен в точке С (AC=0,4 м).

Рис. 164 и 165. Два груза на валу

<< задача 115 || задача 117 >>

Решение задачи

1. Три нагрузки – вес G и грузы Q и Р, приложенные к вороту, уравновешиваются реакциями подшипников А и В. Нагрузки действуют в плоскостях, перпендикулярных к оси вала, и, следовательно, не смещают вал вдоль оси, поэтому и реакции подшипников расположатся в плоскостях, перпендикулярных к этой же оси. Заменим их составляющими XA, ZA и XB, ZB (рис. 164). Следует учесть, что обычный подшипник не создает реакции, направленной вдоль оси вала. Если на вал действуют нагрузки, смещающие вал вдоль оси, то один из подшипников должен быть заменен подпятником.

2. Изобразим ворот со всеми действующими на него силами в трех проекциях (рис. 165 а, б, в) и при помощи их составим уравнения равновесия.

Так же как и в предыдущей задаче, уравнение проекций на ось у превратится в тождество вида 0=0. При составлении уравнения моментов относительно оси у нужно учитывать, что радиус колеса R в четыре раза больше радиуса вала r (R=4r).

Определение величины груза, при котором ворот остается в равновесии