Равновесие произвольной пространственной системы сил(Физика → Теоретическая механика → Пространственная система сил → Задача 115) Условие задачиКвадратная крышка весом 400 н удерживается приоткрытой на 60° над горизонтальной плоскостью противовесом Q (рис. 162). Определить, пренебрегая трением на блоке D, вес противовеса Q и реакции шарниров А и В, если блок D укреплен на одной вертикали с шарниром А и AD=AC.  |
1. Выбрав за начало координат точку А и расположив оси так, как показано на рис. 162, покажем на этом же рисунке активные силы и реакции опор.
На крышку действует сила тяжести G, которую считаем приложенной в точке E (центр симметрии квадрата), и реакция Т нити CD, приложенная в точке С. Сила Т численно равна весу Q противовеса. Действие этих сил уравновешивается реакциями шарниров А и В. Так как силы Т и G действуют в плоскостях, перпендикулярных к оси у, то реакции шарниров лежат в плоскостях, перпендикулярных к той же оси. Поэтому реакцию шарнира А заменим двумя составляющими XA и ZA, а реакцию шарнира В – составляющими XB и ZB.
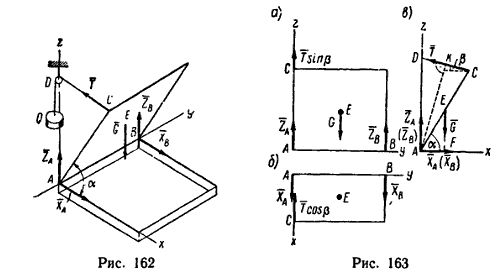
2. Если составление уравнений равновесия по рис. 162 затруднительно, можно предварительно изобразить крышку вместе с действующими на нее силами в трех проекциях, как это сделано на рис. 163:
а) вид спереди, ось х перпендикулярна к плоскости проекции;
б) вид сверху, ось z перпендикулярна к плоскости проекции;
в) вид слева, ось у перпендикулярна к плоскости проекции.
3. Составим уравнения равновесия.
Для составления уравнений проекций на ось х воспользуемся рис. 163, б или 163, в:
Таким образом, чтобы крышка находилась в равновесии приоткрытой под углом 60°, вес противовеса должен быть Q=T=103,5 н. При этом реакция шарнира А имеет две составляющие: горизонтальную XA=100 н и вертикальную ZA=173,2 н, а реакция шарнира В направлена вертикально и равна ZB=200 н.