Решение задачи
1. Давления, производимые колесами, численно равны реакциям опоры, поэтому приложим к каждому колесу перпендикулярно к опорной плоскости реакции RA, RB и RC. Образовалась система четырех параллельных сил, расположенных в пространстве.
2. Расположим оси координат, как показано на рис. 161, и составим уравнения равновесия:
(1) ∑ Zi = 0; RA + RB + RC - P = 0;
(2) ∑ Mx(Pi) = 0; -P*DE + RC*OC = 0;
(3) ∑ My(Pi) = 0; P*DF - RA*OA + RB*OB = 0.
3. Решаем полученную систему уравнений. Из уравнения (2)
RC = P*DE/OC = 8*0,5/1 = 4 кн.
Затем решение можно продолжить так. Подставляя известные числовые значения в уравнения (1) и (3) и перенеся известные члены в правую сторону, получаем такую систему двух уравнений:
(4) RA + RB = 4;
(5) RA*0,4 - RB*0,4 = 8*0,1.
Разделим обе части уравнения (5) на 0,4, тогда система уравнений приобретает такой простой вид:
RA + RB = 4;
RA - RB = 2.
Сложив эти уравнения, найдем RA=3 кн.
Вычтем из первого второе, найдем RB=1 кн.
Как видно, реакции не равны между собой, следовательно, соответственно колеса давят на опорную плоскость также неодинаково.
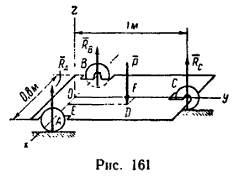 На рис. 161 схематично изображена трехколесная платформа для перевозки грузов. На платформе лежит груз Р=8 кн таким образом, что его вес можно считать приложенным в точке D, причем EO=DF=0,1 м и DE=OF=0,5 м.
На рис. 161 схематично изображена трехколесная платформа для перевозки грузов. На платформе лежит груз Р=8 кн таким образом, что его вес можно считать приложенным в точке D, причем EO=DF=0,1 м и DE=OF=0,5 м.