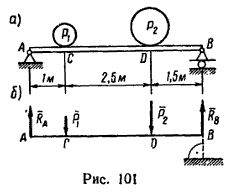
Определение реакции опор балки
1. Рассмотрим равновесие балки АВ, на которую в точках С и D действуют две вертикальные нагрузки P1 и P2 (рис. 101, б).
2. Освободив правый конец балки от связи и заменив ее действие реакцией Rв, направленной перпендикулярно к опорной поверхности, увидим, что на балку действует система параллельных сил. Поэтому, если освободить и левый конец балки от шарнирно неподвижной опоры, то ее реакция будет также направлена вертикально (рис. 101, б).
3. Составим систему уравнений равновесия вида (5), приняв для одного уравнения за центр моментов точку A, а для другого – точку B:
(1) ∑ MA(Pi) = 0; -P1*AC - P2*AD + RB*AB = 0,
(2) ∑ MB(Pi) = 0; +P2*DB + P1*CB - RA*AB = 0.
4. Решая уравнения, из (1) находим
RB = (P1*AC + P2*AD)/AB = (10*1 + 20*3,5)/5 = 16 кн;
из (2)
RA = (P2*DB + P1*CB)/AB = (20*1,5 + 10*4)/5 = 14 кн.
5. Проверим правильность решения, составив уравнение проекций сил на вертикальную ось у:
∑ Yi = 0; RA - P1 - P2 + RB = 0.
Подставляя в это уравнение числовые значения, получаем тождество
14 - 10 - 20 + 16 = 0 или 0 = 0.
Значит задача решена правильно.
Реакции опор:
RA = 14 кн и RB = 16 кн.
При решении задач рекомендуется не пренебрегать проверкой. От правильности определения реакций опор зависит правильность всего остального решения или расчета.