Равновесие трех непараллельных сил(Физика → Теоретическая механика → Плоская система сходящихся сил → Задача 47) Условие задачиБалка АВ поддерживается в горизонтальном положении стержнем CD, наклоненным к балке под углом α=40°; крепления в точках А, С и D шарнирные (рис. 59, а). Определить реакцию шарнира А и усилие, растягивающее стержень CD, если на конце В балки действует вертикальная сила, равная 20 кн. Весом балки и стержня пренебречь.  |
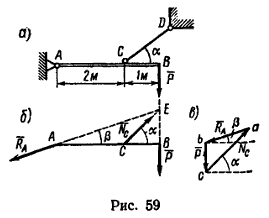
1. На балку действуют три силы (см. рис. 59, а): известная нагрузка Р уравновешивается двумя реакциями: NC – реакцией стержня CD, направленной вдоль стержня, и RA – реакцией шарнира A, направление которой неизвестно.
Построим расчетную схему (рис. 59, б). Отрезок АВ изображает данную балку. На точку В действует вертикальная нагрузка Р. В точке С под углом α=40° на балку действует реакция NC. Направления действия сил Р и NC известны, значит можно получить точку E, в которой пересекаются их линии действия.
В соответствии с теоремой о равновесии трех непараллельных сил через точку Е пройдет и линия действия реакции RA. Значит RA действует вдоль линии ЕА, направленной под углом β к АВ.
2. Силы Р, RA и NC образуют уравновешенную систему. Следовательно, силовой треугольник, построенный из векторов этих сил, должен быть замкнут. Строим треугольник bас (рис. 59, в), в котором отрезок bc изображает силу Р (bc || ВЕ), отрезок са – силу NC(ca || СЕ) и отрезок ab – силу RA(ab || АЕ).
3. Модули сил RA и NC можно определить по теореме синусов, но предварительно необходимо определить углы треугольника abc:
