Равномерное вращательное движение

(Физика → Теоретическая механика → Вращательное движение твердого тела → Задача 163)

Условие задачи

Дисковая пила 1 имеет диаметр 600 мм. На валу пилы насажен шкив 2 диаметром 300 мм, а шкив соединен бесконечным ремнем со шкивом двигателя 3 (рис. 207) диаметром 120 мм. С какой угловой скоростью должен вращаться шкив двигателя, чтобы скорость зубьев пилы не превышала 15 м/сек?

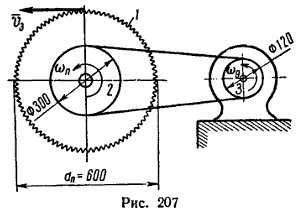
Рис. 207. Скорость шкива и зубьев пилы

<< задача 162 || задача 167 >>

Решение задачи

1. Так как пила 1 и шкив 2 насажены на одном валу, то они имеют одну и ту же угловую скорость ωп и скорость зубьев пилы vз=15 м/сек зависит от ωп:
vз = ωпR или vз = ωпdп/2,
потому что
R = dп/2.

2. Находим угловую скорость шкива 2, который обеспечивает необходимую рабочую скорость зубьев пилы:
ωп = 2vз/dп = 2*15/0,6 = 50 рад/сек (dп = 600 мм = 0,6 м).

3. Теперь найдем угловую скорость ωд шкива двигателя.

Шкивы 2 и 3 соединены бесконечным ремнем. Полагая, что ремень не растягивается и не проскальзывает на шкивах, можно считать, что все его точки движутся с одной и той же скоростью vр. Это означает, что скорости точек, расположенных на поверхностях обоих шкивов, одинаковы и равны vр.

Поэтому применим зависимость v=ωR:
vр = ωпd2/2 = ωдd3/2.

Отсюда
ωд = ωпd2/d3 = 50*300/120 = 125 рад/сек.

4. Если перевести эту угловую скорость в об/мин, то
nд = 30*ωд/π = 30*125/3,14 ≈ 1200 об/мин.

Таким образом, для того чтобы зубья пилы имели скорость 15 м/сек, шкив двигателя должен вращаться с угловой скоростью 125 рад/сек или 1200 об/мин.

* Полученное отсюда отношение угловых скоростей, численно равное обратному отношению их диаметров ωд/ωп=d2/d3, называют передаточным числом ременной передачи.