Равномерное вращательное движение

(Физика → Теоретическая механика → Вращательное движение твердого тела → Задача 162)

Условие задачи

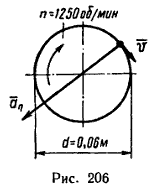
Вал, диаметр которого 0,06 м, вращается равномерно и делает 1200 об/мин. Определить скорость и ускорение точек вала на его поверхности (рис. 206).

Рис. 206. Определить скорость и ускорение на поверхности вала

<< задача 161 || задача 163 >>

Решение задачи

1. Скорость точки вращающегося тела можно найти по формуле
v = ωR.

2. Но известно, что
ω = πn/30.

3. Поэтому
v = πnR/30.

4. Подставим сюда R=d/2=0,06/2=0,03 м и n=1200 об/мин:
v = πnR/30 = 3,14*1200*0,03/30 = 3,77 м/сек.

Вал вращается равномерно, значит скорость точек остается численно неизменной. По этой же причине у точек отсутствует касательное ускорение.

5. Нормальное ускорение найдем из формулы
an = v2/R = 3,772/0,03 = 474 м/сек2,
которое также в данном случае остается по модулю неизменным.