Многоугольник сил. Определение равнодействующей сходящихся сил

(Физика → Теоретическая механика → Плоская система сходящихся сил → Задача 36)

Условие задачи

Определить равнодействующую пяти сил:
P1 = 52 н, P2 = 70 н, P3 = 69 н, P4 = 77 н, P5 = 70 н,
действующих на точку А, как показано на рис. 45, а.

<< задача 35 || задача 39 >>

Решение методом проекций

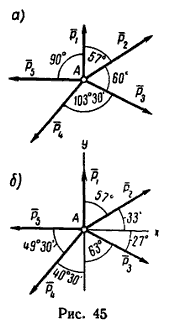
Рис. 45. Пять силь приложены в одну точку

1. Так как силы P1 и P5 направлены друг к другу под прямым углом, то и совместим с этими силами ось проекций. Тогда векторы P2, P3 и 4 будут образовывать с осями проекций углы, показанные на рис. 45, б.

2. Найдем проекцию равнодействующей на ось х:
XR = P2 cos 33° + P3 cos 27° - P4 cos 49°30' - P5 = 70 cos 33° + 69 cos 27° - 77 cos 49°30' - 70 = 58,6 + 61,4 - 50 - 70 = 0.

3. Найдем проекцию равнодействующей на ось у:
YR = P1 + P2 sin 33° - P3 sin 27° - P4 sin 49°30' = 52 + 70 sin 33° - 69 sin 27° - 77 sin 49°30' = 52 + 38 - 31,4 - 58,6 = 0.

4. Обе проекции искомой равнодействующей равны нулю, значит и сама равнодействующая также равна нулю.

Таким образом, данная система сил уравновешена. Иными словами, любую из пяти заданных сил можно рассматривать как уравновешивающую четыре остальных.