Равновесие сходящихся сил

(Физика → Теоретическая механика → Плоская система сходящихся сил → Задача 39)

Условие задачи

Фонарь весом 9 кГ подвешен на кронштейне ABC (рис. 48, а). Определить реакции горизонтального стержня АВ и наклонной тяги ВС, если AB=1,2 м и BC=1,5 м; крепления в точках А, В и С шарнирные.

<< задача 36 || задача 40 >>

Решение графо-аналитическим методом с применением геометрических соотношений

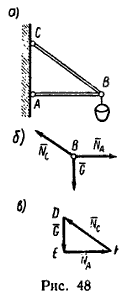
Рис. 48. Фонарь подвешен на кронштейне

1. В данном случае на шарнир В действуют три силы: вес фонаря G (рис. 48, б) и реакции стержней NA и NC, направленные вдоль стержней. Заметим, что стержень АВ сжат, значит реакция NA направлена от стержня к шарниру, а стержень ВС растянут, поэтому реакция NC направлена от шарнира к стержню. Шарнир В с действующими на него силами изобразим отдельно.

2. Так как шарнир В под действием этих трех сил находится в равновесии, силовой треугольник, составленный из них, должен быть замкнутым.

Выберем произвольную точку D (рис. 48, в) и отложим от нее отрезок DE, изображающий силу G. Из точек Е и D проведем прямые EF и DF, параллельные соответственно АВ и СВ. В полученном треугольнике DEF сторона EF изображает реакцию NA (реакцию стержня АВ) и сторона FD – реакцию NC (реакцию стержня ВС)*.

3. Так как в условии задачи даны линейные размеры кронштейна, величины сил NA и NC наиболее просто определить исходя из подобия треугольников ABC и EFD:
BC/NC = BA/NA = AC/G.

Отсюда
NC = G*BC/AC и NA = G*BA/AC.

4. Неизвестную в задаче длину АС определяем по теореме Пифагора:
AC = sqrt(BC2 - BA2) = sqrt(1,52 - 1,22) = 0,9 м.

5. Окончательно
NC = 9*1,5/0,9 = 15 кГ и NA = 9*1,2/0,9 = 12 кГ.

* Если все указанные в п. 2 построения выполнить в определенном масштабе, а затем измеренные длины EF и FD умножить на масштаб построения, то получим решение задачи графическим методом.