Правило параллелепипеда сил

(Физика → Теоретическая механика → Пространственная система сил → Задача 107)

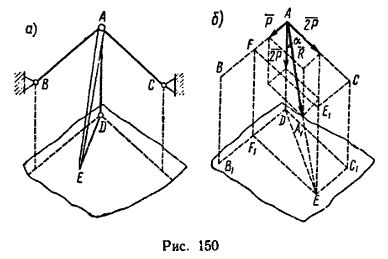
Условие задачи

Три цепи одинаковой длины l соединены вместе кольцом А (рис. 150, а). Оставшиеся свободными концы цепей закреплены в трех точках В, С и D таким образом, что эти точки образуют вершины куба. Как необходимо установить под кольцо А подпорку АЕ и какую длину она должна иметь, чтобы кольцо А располагалось относительно точек В, С и D как четвертая вершина куба? При этом цепь АВ должна быть натянута силой Р, а цепи AD и АС – силами 2Р каждая. Определить также усилие в подпорке АЕ. Весом подпорки пренебречь.

Рис. 150. Цепи, кольцо и подпорка

<< задача 104 || задача 108 >>

Решение задачи

1. Из точки А (рис. 150, б) вдоль цепей отложим заданные силы: вдоль цепи АВ – силу Р, вдоль цепей АС и AD – силы 2Р. Построив на них параллелепипед, получим в нем диагональ АА1, выражающую равнодействующую трех усилий в цепях.

Вдоль линии действия равнодействующей R нужно установить подпорку АЕ, которая должна соответствовать диагонали параллелепипеда ACE1FDC1EF1, подобного силовому параллелепипеду.

2. Находим модуль равнодействующей:
R = sqrt(P12 + P22 + P32) = sqrt(P2 + 2(2P)2) = sqrt(P2 + 8P2) = 3P.

3. Из подобия двух показанных на рис. 150, б параллелепипедов следует пропорция
AC/2P = AF/P = AE/R.
Зная, что длина цепи AC=l, находим длину подпорки АЕ:
AE = R*AC/(2P) = 3l/2,
а также расстояние AF=C1E:
AF = AC/2 = l/2.

Таким образом, усилие в подпорке равно 3Р, длина подпорки 1,5l, а установить ее нужно так, чтобы нижний конец Е находился от DB1 на расстоянии F1E=l и от DC1 – на расстоянии C1E=AF=l/2.

Решение этой задачи после выполнения пункта 2 можно продолжать иным путем. Можно найти угол α, образуемый R с вертикальной цепью, а затем определить из ΔADE длину АЕ и т. д.