Правило параллелепипеда сил

(Физика → Теоретическая механика → Пространственная система сил → Задача 108)

Условие задачи

Найти усилия в стержне АВ и цепях АС и AD, поддерживающих груз Q весом 42 кГ, если АВ=145 см, АС=80 см, AD=60 см. Плоскость прямоугольника CADE горизонтальна, а плоскости V и W вертикальны. Крепление в точке В шарнирное (рис. 151, а).

Рис. 151. Найти усилия в стержне и цепях

<< задача 107 || задача 109 >>

Решение задачи

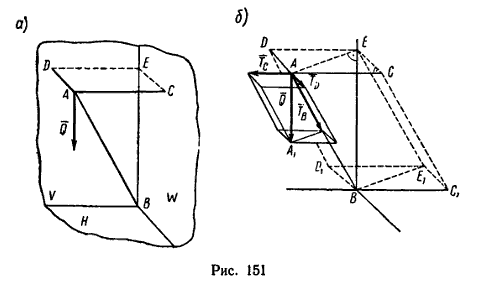
1. Разложим силу Q на три составляющие TB, TC и TD, направленные соответственно вдоль стержня AB и цепей АС и AD. Для этого, приняв вектор Q за диагональ АА1, построим силовой параллелепипед, из которого видно, что составляющая TB сжимает стержень АВ, а составляющие TC и TD растягивают цепи АС и AD (рис. 151, б).

2. Соответственно приняв отрезок BE за диагональ, а стержень АВ и цепи АС и AD – за ребра, построим параллелепипед, подобный силовому (см. рис. 151, б).

3. Из подобия параллелепипедов, полученных на рис. 151, б, следует пропорция
(а) Q/BE = TC/AC = TD/AD = TB/AB.

4. Длины трех отрезков из четырех, входящих в пропорцию, известны. Длина отрезка BE неизвестна. Найдем ее из рассмотрения прямоугольных треугольников ABE и АСЕ:
BE2 = AB2 - AE2 = AB2 - (AC2 + CE2) = AB2 - AC2 - AD2,
откуда
BE = sqrt(AB2 - AC2 - AD2) = sqrt(1452 - 802 - 602) = 105 см.

5. Рассматривая теперь первое отношение пропорции (а) вместе со вторым, а затем с третьим и четвертым, находим
TC = Q*AC/BE = 42*80/105 = 32 кГ;
TD = Q*AD/BE = 42*60/105 = 24 кГ;
TB = Q*AB/BE = 42*145/105 = 58 кГ.