linda
Новичок
|
    
огромное спасибо!!!
|
Всего сообщений: 4 | Присоединился: ноябрь 2009 | Отправлено: 6 нояб. 2009 20:24 | IP
|
|
bin0m
Новичок
|
Помогите разрешить спор.
Легенькая задачка, но мы с приятелем умудрились поспорить, и уже запутались...
------------
3 одинаковых шарика раскидывают по 3 одинаковым корзинкам. Какова вероятность, что 3 шарика будут в одной корзинке?
---------------
Есть всего 3 возможные комбинаци: 1-1-1, 2-1-0,3-0-0
Значит вероятность, что выпадет один из них равна 1/3 .... но если считать варианты каждого шарика по шагам, то видно, что 2-1-0, значительно чаще случаеться...
Помогите разобраться, пожайлуста!
|
Всего сообщений: 1 | Присоединился: ноябрь 2009 | Отправлено: 11 нояб. 2009 15:36 | IP
|
|
ProstoVasya
Долгожитель
|
После того как один шарик куда-то попал, остальным нужно попасть туда же. Поэтому вероятность равна 1/3*1/3 = 1/9
Можно иначе. Занумеруем корзины. Любой из шариков может попасть в любую корзину. Т.е. результатом опыта будет упорядоченный набор из трёх чисел - номеров корзин куда попали шары. Число вариантов (таких троек) 27. Среди них благоприятные те, у которых номера корзин совпадают, т.е. три варианта. Ответ 3/27 = 1/9.
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 11 нояб. 2009 23:31 | IP
|
|
Izymrydik
Новичок
|
1)На книжной полке два отделения. Сколько способов расставить 5 разных книг, если сначала нужно поставить три книги в первое отделение, а затем две во второе?
2)У одного коллекционера 10 редких марок, у другого 8. Сколько существует способов обмена друг с другом не менее чем по 8 марок?Помогите решить пожалуйста! ))
|
Всего сообщений: 1 | Присоединился: ноябрь 2009 | Отправлено: 29 нояб. 2009 14:28 | IP
|
|
muzz
Новичок
|
помогите пожалуйста с задачкой :в колоде 36 карт.наудачу вынимают 3 карты .каково число всех возможных комбинаций ?сколько троек содержат,по крайней мере,один туз?сколько троек содержат только один туз??заранее спасибо тому кто выручит !
|
Всего сообщений: 1 | Присоединился: ноябрь 2009 | Отправлено: 29 нояб. 2009 22:25 | IP
|
|
daemoon
Новичок
|
Подскажите пожалуста как решить данную задачу:
Найти число всех таких слов длинны mxn в n-буквенном алфавите, в которых каждая буква встречается m раз.
(Сообщение отредактировал daemoon 9 дек. 2009 23:57)
|
Всего сообщений: 3 | Присоединился: декабрь 2009 | Отправлено: 9 дек. 2009 23:50 | IP
|
|
llorin1
Участник
|
Каждое из m мест в mxn слове сочетается с оставшимися mn-m местами:
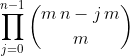
(Сообщение отредактировал llorin1 10 дек. 2009 12:47)
|
Всего сообщений: 147 | Присоединился: июнь 2006 | Отправлено: 10 дек. 2009 12:44 | IP
|
|
daemoon
Новичок
|
Спасибо большое!!!!!
|
Всего сообщений: 3 | Присоединился: декабрь 2009 | Отправлено: 10 дек. 2009 15:38 | IP
|
|
HELEN
Новичок
|
Здравствуйте! Ребята, помогите, пожалуйста решить задачки. Очень срочно нужно.
1. Сколькими способами можно распределить n различных открыток в k 1) различных,
2)неразличимых конвертов, если а) все конверты не пусты,
b)допускаются пустые конверты.
2. Сколько различных слов можно получить перестановкой букв слова L, где а) L-министр, условие, нельзя сказать, что согласные идут в алфавитном порядке;
b)L- слово переворот..., условие не больше 1-ой пары одинаковых букв стоят рядом.
3.Сколькими способами из колоды карт в 36 листов можно выбрать неупорядоченный набор из 5 карт так, чтобы в этом наборе было бы точно... три короля, 2 бубновых карты.
В 1 номере n=7, k=3/
(Сообщение отредактировал attention 14 дек. 2009 7:35)
|
Всего сообщений: 2 | Присоединился: декабрь 2009 | Отправлено: 11 дек. 2009 17:30 | IP
|
|
Dasha17
Новичок
|
Здравствуйте)))Помогите ,пожалуйста,решить несколько задачек
1.12 человек голосуют за 2 кандидатов, причем каждый голосует либо ровно за одного из них, либо против обоих. Сколькими способами могут распределиться голоса избирателей, если учитывается только количество голосов, поданных за каждого претендента?
2.Из города A в город B ведут 8 дорог, из города B в город C-5 дорог, а из города A в город C-11 дорог. Путешественник вышкл из пункта A, и пройдя ровно по 3 дорогам вновь вернулся в пункт A. Сколькими способами он мог это сделать?
|
Всего сообщений: 1 | Присоединился: декабрь 2009 | Отправлено: 13 дек. 2009 17:09 | IP
|
|
|
Форум
2.8.3 Комбинаторика
