faust2
Новичок
|
     
ProstoVasya
Спасибо за объяснение !
Сколько существует пятизначных номеров (номера могут начинаться с нуля), у которых:
а) ровно один раз встречается цифра 2?
б) цифры убывают?
в) не встречается одинаковых подряд стоящих цифр?
а) сумма цифр четна?
б) сумма цифр на четных местах больше 10?
в) все цифры четные?
(Сообщение отредактировал attention 14 дек. 2009 7:24)
|
Всего сообщений: 9 | Присоединился: июнь 2009 | Отправлено: 5 июля 2009 12:42 | IP
|
|
Xinata
Новичок
|
Помогите пожалуйста решить задачу. Сколько сушествует пятизначных номеров телефона используя 10 цифр т.е (0,1,2,3,4,5,6,7,8,9)
1) Исключая 0 вообще
2) Исключая 0 только на первом месте
|
Всего сообщений: 1 | Присоединился: сентябрь 2009 | Отправлено: 4 сен. 2009 19:50 | IP
|
|
RKI 
Долгожитель
|
Цитата: Xinata написал 4 сен. 2009 19:50
Помогите пожалуйста решить задачу. Сколько сушествует пятизначных номеров телефона используя 10 цифр т.е (0,1,2,3,4,5,6,7,8,9)
1) Исключая 0 вообще
2) Исключая 0 только на первом месте
1) 9^5 = 59 049
2) 9*(10^4) = 90 000
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 5 сен. 2009 13:09 | IP
|
|
lamama
Новичок
|
Здравствуйте, помогите пожалуйста решить задания! Нужно решить до завтрашнего вечера, очень прошу, никогда раньше не изучал теорию вероятностей, поэтому вся надежда на Вас:
Здесь сканы задания, очень прошу помочь...
(Сообщение отредактировал attention 14 дек. 2009 7:27)
|
Всего сообщений: 2 | Присоединился: сентябрь 2009 | Отправлено: 15 сен. 2009 23:47 | IP
|
|
RKI
Долгожитель
|
Цитата: lamama написал 15 сен. 2009 23:47
Здравствуйте, помогите пожалуйста решить задания! Нужно решить до завтрашнего вечера, очень прошу, никогда раньше не изучал теорию вероятностей, поэтому вся надежда на Вас:
Здесь сканы задания, очень прошу помочь...
Задание 1.
A = {не менее трех девочек}
A = A1 + A2 + A3, где
A1 = {три девочки и два мальчика}
A2 = {четыре девочки и один мальчик}
A3 = {пять девочек}
Найдем вероятности событий A1, A2, A3. Посчитаем число n всевозможных исходов. Всего в классе 10+8 = 18 учеников. Способов выбрать 5 человек из 18 имеющихся
n = C(5;18) = 18!/5!13! = 8 568
Посчитаем число m событий, благоприятных событию A1. Способов выбрать 3 девочки из 8 имеющихся
m1 = C(3;8) = 8!/3!5! = 56.
Способов выбрать 2 мальчика из 10 имеющихся
m2 = C(2;10) = 10!/2!8! = 45.
По правилу произведения m = m1*m2 = 56*45 = 2 520
Посчитаем число k событий, благоприятных событию A2. Способов выбрать 4 девочки из 8 имеющихся
k1 = C(4;8) = 8!/4!4! = 70.
Способов выбрать 1 мальчика из 10 имеющихся
k2 = C(1;10) = 10!/1!! = 10.
По правилу произведения k = k1*k2 = 70*10 = 700.
Посчитаем число l событий, благоприятных событию A3. Способов выбрать 5 девочек из 8 имеющихся
l = C(5;8) = 8!/5!3! = 56.
По классическому определению вероятности
P(A1) = m/n = 2520/8568
P(A2) = k/n = 700/8568
P(A3) = l/n = 56/8568
P(A) = P(A1 + A2 + A3) = [события A1, A2 и A3 несовместны] =
= P(A1) + P(A2) + P(A3) = 2520/8568 + 700/8568 + 56/8568 =
= 3276/8568 = 13/34
P.S. Учитывайте Ваши правила оформления (я просто написала ход решения).
Цитата: lamama написал 15 сен. 2009 23:47
Здравствуйте, помогите пожалуйста решить задания! Нужно решить до завтрашнего вечера, очень прошу, никогда раньше не изучал теорию вероятностей, поэтому вся надежда на Вас:
Здесь сканы задания, очень прошу помочь...
Задание 2.
X 10.1 10.2 10.4 10.7 11.1
P 0.5 0.2 0.1 0.1 0.1
математическое ожидание
M(X) = (10.1)*(0.5) + (10.2)*(0.2) + (10.4)*(0.1) +
+ (10.7)*(0.1) + (11.1)*(0.1) =
= 5.05 + 2.04 + 1.04 + 1.07 + 1.11 = 10.31
M(X^2) = (102.01)*(0.5) + (104.04)*(0.2) + (108.16)*(0.1) +
+ (114.49)*(0.1) + (123.21)*(0.1) =
= 51.005 + 20.808 + 10.816 + 11.449 + 12.321 = 106.399
дисперсия
D(X) = M(X^2) - (M(X))^2 = 106.399 - 106.2961 = 0.1029
среднее квадратическое отклонение
б(X) = sqrt(D(X)) = sqrt(0.1029) ~ 0.320780299...
Функция распределения случайной величины X имеет вид:
F(x) = {0, x <= 10.1
{0.5, 10.1 < x <= 10.2
{0.7, 10.2 < x <= 10.4
{0.8, 10.4 < x <= 10.7
{0.9, 10.7 <x <= 11.1
{1, x > 11.1
P.S. Учитывайте Вам указанные правила оформления (я просто написала ход решения). График функции распределения постройте по указанной Выше формуле (вид графика - ступенька)
Задание 3
x* = ( -1.0 - 0.8 - 0.6 - 0.4 - 0.2 - 0.0 + 0.2 + 0.4 + 0.6 + 0.8 + 1.0 + 1.2 + 1.4 + 1.6 + 1.8)/15 = 6/15 = 0.4
(-1.0-0.4)^2 + (-0.8-0.4)^2 + (-0.6-0.4)^2 + (-0.4-0.4)^2 + (-0.2-0.4)^2 + (0.0-0.4)^2 + (0.2-0.4)^2 + (0.4-0.4)^2 + (0.6-0.4)^2 + (0.8-0.4)^2 + (1.0-0.4)^2 + (1.2-0.4)^2 + (1.4-0.4)^2 + (1.6-0.4)^2 + (1.8-0.4)^2 =
= 1.96 + 1.44 + 1 + 0.64 + 0.36 + 0.16 + 0.04 + 0 + 0.04 + 0.16 + 0.36 + 0.64 + 1 + 1.44 + 1.96 = 11.2
y* = (- 1.2 - 1.8 - 2.7 - 3.4 - 3.6 - 2.9 - 2.4 - 2.1 - 0.4 + 1.1 + 2.8 + 4.6 + 6.5 + 6.4 + 8.3)/15 = (9.2)/15
(-1.0-0.4)*(-1.2-(9.2)/15) + (-0.8-0.4)*(-1.8-(9.2)/15) + (-0.6-0.4)*(-2.7-(9.2)/15) + (-0.4-0.4)*(-3.4-(9.2)/15) + (-0.2-0.4)*(-3.6-(9.2)/15) + (0.0-0.4)*(-2.9-(9.2)/15) + (0.2-0.4)*(-2.4-(9.2)/15) + (0.4-0.4)*(-2.1-(9.2)/15) + (0.6-0.4)*(-0.4-(9.2)/15) + (0.8-0.4)*(1.1-(9.2)/15) + (1.0-0.4)*(2.8-(9.2)/15) + (1.2-0.4)*(4.6-(9.2)/15) + (1.4-0.4)*(6.5-(9.2)/15) + (1.6-0.4)*(6.4-(9.2)/15) + (1.8-0.4)*(8.3-(9.2)/15) =
= (-1.4)*((-27.2)/15) + (-1.2)*(-(36.2)/15) + (-1)*(-(49.7)/15) + (-0.8)*(-(60.2)/15) + (-0.6)*(-(63.2)/15) + (-0.4)*(-(52.7)/15) + (-0.2)*(-(45.2)/15) + 0 + (0.2)*(-(15.2)/15) + (0.4)*((7.3)/15) + (0.6)*((32.8)/15) + (0.8)*((59.8)/15) + 1*((88.3)/15) + (1.2)*((86.8)/15) + (1.4)*((115.3)/15) =
= (38.08)/15 + (43.44)/15 + (49.7)/15 + (48.16)/15 + (37.92)/15 + (21.08)/15 + (9.04)/15 - (3.04)/15 + (2.92)/15 + (19.68)/15 + (47.84)/15 + (88.3)/15 + (104.16)/15 + (161.42)/15 =
= (668.7)/15 = 44.58
b = (44.58)/(11.2) = 2229/560
a = (9.2)/15 - (2229/560)*(0.4) = (9.2)/15 - 2229/1400 =
= 12880/21000 - 33435/21000 = - 20555/21000 =
= - 4111/4200
y = a + bx
y = 2229x/560 - 4111/4200
y = (1/4200)*((16717.5)x - 4111)
хотя я немного сомневаюсь
(Сообщение отредактировал attention 14 дек. 2009 7:32)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 16 сен. 2009 11:15 | IP
|
|
linka4583
Новичок
|
Пмогите решить задачку!!
Cколькими способами можно распределить 5апельсинов, 4 банана, 1 яблоко, 1 грушу, 2 ананаса на 5 человек? Людей различать.
|
Всего сообщений: 3 | Присоединился: сентябрь 2009 | Отправлено: 17 сен. 2009 16:43 | IP
|
|
ProstoVasya
Долгожитель
|
В комбинаторике есть формула для вычисления числа раскладов n неразличимых шаров по k (различимым) ящикам . Это число вычисляется по формуле C(n,n+k-1) - число сочетаний по n из n+k-1.
Число способов распределения апельсин (n =5, k=5) равно С(5,9) = 126,
число способов распределения бананов (n =4, k=5) равно С(4,8) = 70, число способов распределения яблок (n =1, k=5) равно С(1,5) = 5,
число способов распределения груш (n = 1, k =5) равно С(1,5) = 5,
число способов распределения ананасов (n=2, k=5) равно С(2,6) =15.
Теперь все эти числа надо перемножить
126*70*5*5*15 = 3307500.
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 17 сен. 2009 18:43 | IP
|
|
linka4583
Новичок
|
Большое спасибо)))
|
Всего сообщений: 3 | Присоединился: сентябрь 2009 | Отправлено: 17 сен. 2009 23:25 | IP
|
|
aido
Долгожитель
|
ребят, помогите упростить сумму:
n
sigma(Cn(k)*Ck(q))
k=q
то, что в скобках - это верхний индекс, без скобок - нижний. то есть читается: Cn(k) - сочетание из n элементов по k.
|
Всего сообщений: 569 | Присоединился: сентябрь 2008 | Отправлено: 28 сен. 2009 22:59 | IP
|
|
llorin1
Участник
|
!\cdot (k - q)! } =)
заменив индекс суммирования i=k-q, запишем:
!\cdot i!}=\frac{n!}{(n-q)!\cdot q!}\sum _{i=0}^{n-q}\frac{(n-q)!}{(n-q-i)!\cdot i!}=C_n^q\sum_{i=0}^{n-q}C_{n-q}^i =)
используя бином Ньютона, получим
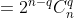
(Сообщение отредактировал attention 14 дек. 2009 7:33)
|
Всего сообщений: 147 | Присоединился: июнь 2006 | Отправлено: 29 сен. 2009 9:38 | IP
|
|
|
Форум
2.8.3 Комбинаторика
