RKI 


Долгожитель
|
     
Цитата: hfgeasd написал 28 сен. 2009 17:49
sqrt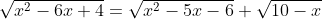
Решить уравнение
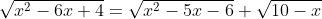
(10 - x)} )
(x-6)(10-x)} )
(x-6)(10-x)} = 0 )
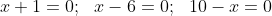
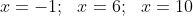
Проверка
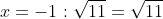
Следовательно, x=-1 является корнем уравнения
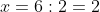
Следовательно, x=6 является корнем уравнения
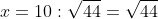
Следовательно, x=10 также является корнем уравнения
(Сообщение отредактировал attention 7 дек. 2009 6:30)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 28 сен. 2009 18:13 | IP
|
|
hfgeasd


Новичок
|
      
Решить уравнение и в ответ записать сумму его корней
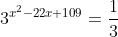
(Сообщение отредактировал attention 7 дек. 2009 6:31)
|
Всего сообщений: 32 | Присоединился: сентябрь 2009 | Отправлено: 28 сен. 2009 18:22 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: hfgeasd написал 28 сен. 2009 18:22
Решить уравнение и в ответ записать сумму его корней
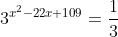
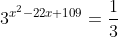
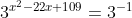
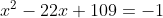
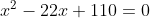
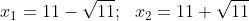
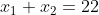
(Сообщение отредактировал attention 7 дек. 2009 6:32)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 28 сен. 2009 18:27 | IP
|
|
Alventa


Новичок
|
       
Есть два примера, вызвавших трудности, подскажите пожалуйста, как их решать
3(x-2)+4*sqrt(2x^2-3x+1)-2(x^2-1)=0
я пробовала корень оставить в левой части, а все остальное переносить в правую и возводила в квадрат.
16(2x^2-3x+1)=9(x-2)^2-12(x-2)*(x^2-1)+4(x^2-1)^2
если раскрыть все скобки, то получается
4x^4-12x^3-7x^2+24x=0
а что дальше - не очень ясно. Можно конечно долго и нудно искать корни схемой Горнера, но мне кажется, что здесь должно быть решение проще, например заменой, но мне его увидеть не удалось(
И второй пример:
1/(2х+3) - 1/(х^2-16) + 1/(х^2+11х+12) - (х-8)/[(2х+3)*(х^2-16)] =0
Привожу к общему знаменателю, получаю страшную дробь, числитель которой должен быть равен нулю, а знаменатель, соответственно, не равен. Но меня сейчас интересует только числитель
(х^2-16)*(х^2+11х+12) - (2х+3)*(х^2+11х+12) + (х^2-16)*(2х+3) - (х-8)*(х^2+11х+12)=0
Дальше логично предположить замену или группировку, но группировка ничего не даёт(все равно до конца на множители не раскладывается), а с заменой у меня тоже ничего не вышло - скобка (х^2+11х+12) везде всё портит
я пробовала раскрыть скобки
х^4+10х^3-41х^2-177х-180=0
и опять получается уравнение неудоборешаемое =(
|
Всего сообщений: 6 | Присоединился: январь 2009 | Отправлено: 13 окт. 2009 17:28 | IP
|
|
paradise 

Долгожитель
|
       
Цитата: Alventa написал 13 окт. 2009 17:28
Есть два примера, вызвавших трудности, подскажите пожалуйста, как их решать
3(x-2)+4*sqrt(2x^2-3x+1)-2(x^2-1)=0
я пробовала корень оставить в левой части, а все остальное переносить в правую и возводила в квадрат.
16(2x^2-3x+1)=9(x-2)^2-12(x-2)*(x^2-1)+4(x^2-1)^2
если раскрыть все скобки, то получается
4x^4-12x^3-7x^2+24x=0
а что дальше - не очень ясно. Можно конечно долго и нудно искать корни схемой Горнера, но мне кажется, что здесь должно быть решение проще, например заменой, но мне его увидеть не удалось(
3(x-2) + 4*sqrt(2x^2-3x+1) - 2(x^2-1) = 0
4*sqrt(2x^2-3x+1) = 2(x^2-1) - 3(x-2)
4*sqrt(2x^2-3x+1) = 2x^2-2-3x+6
4*sqrt(2x^2-3x+1) = 2x^2-3x+4
Замена: 2x^2-3x+1 = t, t>=0
4*sqrt(t) = t+3
16t = t^2+6t+9
t^2+6t+9-16 = 0
t^2+6t-7 = 0
D = 36-4*1*(-7) = 36+28 = 64
t1 = (-6+8)/2 = 1
t2 = (-6-8)/2 = -7 - не удовлетворяет условию t >= 0
2x^2-3x+1 = 1
2x^2-3x = 0
x(2x-3) = 0
x1 = 0; x2 = 1.5
|
Всего сообщений: 428 | Присоединился: ноябрь 2008 | Отправлено: 13 окт. 2009 17:59 | IP
|
|
Alventa


Новичок
|
       
to paradise, спасибо большое
|
Всего сообщений: 6 | Присоединился: январь 2009 | Отправлено: 14 окт. 2009 14:59 | IP
|
|
ProstoVasya

Долгожитель
|
     
Alventa
Видимо в условии второй задачи произошла опечатка. Если свести дело к уравнению четвёртой степени, то получим уравнение
х^4+10х^3-29х^2-189х-180=0
Здесь можно воспользоваться методом (формулами) Феррари. Получим четыре корня, выраженные сложными радикалами.
Метод Феррари состоит в том, многочлен раскладывается в произведение квадратных многочленов. Коэффициенты этих многочленов тоже выглядят громоздко.
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 14 окт. 2009 22:50 | IP
|
|
hfgeasd


Новичок
|
      
Решить уравнение
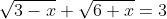
и в ответе записать больший его корень
Решить уравнение
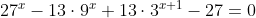
и в ответе записать сумму его корней
(Сообщение отредактировал attention 7 дек. 2009 6:35)
|
Всего сообщений: 32 | Присоединился: сентябрь 2009 | Отправлено: 19 окт. 2009 19:40 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: hfgeasd написал 19 окт. 2009 19:43
Решить уравнение

и в ответе записать сумму его корней
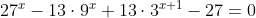
 - 13\cdot(9^{x} - 3^{x+1}) = 0 )
 - 13\cdot(3^{2x} - 3\cdot3^{x}) = 0 )
(3^{2x} + 3\cdot3^{x} + 9) - 13\cdot3^{x}(3^{x} - 3) = 0 )
(3^{2x} + 3\cdot3^{x} + 9 - 13\cdot3^{x}) = 0 )
(3^{2x} - 10\cdot3^{x} + 9) = 0 )
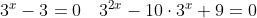
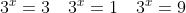
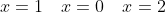
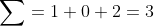
(Сообщение отредактировал attention 8 дек. 2009 1:08)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 19 окт. 2009 20:58 | IP
|
|
paradise 

Долгожитель
|
       
Цитата: hfgeasd написал 19 окт. 2009 22:49
Решить уравнение
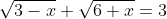
и в ответе записать больший его корень

(Сообщение отредактировал attention 7 дек. 2009 6:38)
|
Всего сообщений: 428 | Присоединился: ноябрь 2008 | Отправлено: 20 окт. 2009 0:19 | IP
|
|

 Форум
Форум

 Математика
Математика

 1.7 Алгебраические уравнения
1.7 Алгебраические уравнения

 Форум
Форум

 Математика
Математика

 1.7 Алгебраические уравнения
1.7 Алгебраические уравнения