Разложение силы на две составляющие

(Физика → Теоретическая механика → Плоская система сходящихся сил → Задача 22)

Условие задачи

Фонарь весом 80 н подвешен на кронштейне ABC, укрепленном на вертикальной стене (рис. 27). Определить усилия, возникшие в горизонтальном стержне СВ и наклонной тяге AB после подвески фонаря, если CB=1 м и AB=1,2 м. Соединения в точках A, B и C кронштейна – шарнирные.

Рис. 27. Кронштейн, укрепленный на стене

<< задача 20 || задача 23 >>

Решение 1 (графическим методом по правилу параллелограмма)

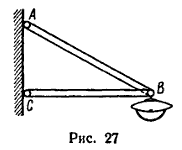
1. Если избран графический метод решения, то прежде всего необходимо в масштабе построить кронштейн ABC. Выполнение чертежа кронштейна сводится, как это следует из формы и размеров, заданных в условии задачи, к построению прямоугольного треугольника по двум заданным сторонам.

2. Построим кронштейн в масштабе "1 м в 44 мм". Обозначив масштаб чертежа μl, выразим зависимость между истинной длиной 1 м и длиной отрезка на чертеже 44 мм:

Определение усилий в стержне и тяге графическим методом по правилу параллелограмма

Как видно из получившегося на рис. 28 построения, тяга AB кронштейна растягивается силой, равной 144 н, а стержень BC сжимается силой 120 н.



Решение 2 (графо-аналитическим методом по правилу параллелограмма с использованием геометрических соотношений)

Определение усилий графо-аналитическим методом

Таким образом, результат практически тот же, что и при графическом решении. Некоторое расхождение объясняется меньшей точностью графического решения.

Как уже известно, графо-аналитическое решение задачи 22 основано на подобии двух треугольников: кронштейна, имеющего вид треугольника, и силового треугольника. Но возможен случай, когда на чертеже нагруженного устройства или конструкции не будет треугольника, подобного силовому. Тогда для решения задачи целесообразно применить графо-аналитический метод с использованием тригонометрических соотношений (см. задачу 23).