Равновесие произвольной пространственной системы сил

(Физика → Теоретическая механика → Пространственная система сил → Задача 118)

Условие задачи

На вале редуктора жестко укреплены два зубчатых колеса: коническое 1 и цилиндрическое 2 (рис. 169, а). Левая цапфа вала опирается на подшипник, воспринимающий только радиальную силу давления, действующую перпендикулярно к оси вала, а правая цапфа (пята) опирается на подпятник, т. е. на опору, способную, кроме радиальной силы давления, воспринимать и осевую (силу, действующую вдоль оси вала).

На колесо 1 действуют три силы: касательная P1=4 кн (окружное усилие); радиальная Q1=1,28 кн и осевая S1=0,48 кн. Определить в положении равновесия силы P2 и Q2=0,36 P2, приложенные к колесу 2, а также реакции опор A и В. Необходимые размеры (в мм) даны на рис. 169, а. Весом вала и колес пренебречь.

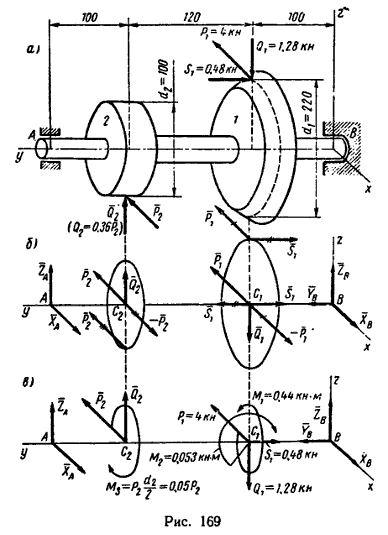
Рис. 169. Нагрузки на редуктор

<< задача 117 || задача 122 >>

Решение задачи

1. Заданные и искомые силы, приложенные к колесам 1 и 2, приведем к точкам С1 и С2 на геометрической оси вала (рис. 169, б).

Сила Q1=1,28 кн, действующая вдоль радиуса колеса, переносится в точку С1 непосредственно. Для приведения к точке С1 силы P1=4 кн, приложим к этой точке уравновешенную систему сил P1 и -P1 и тогда, кроме приведенной силы P1, образуется пара сил (P1; -P1), отмеченная на рисунке одной черточкой (присоединенная пара сил). При переносе в точку С1 силы S1=0,48 кн аналогичным образом появляется пара (S1; -S1) отмеченная двумя черточками. Сила Q2, действующая вдоль радиуса колеса 2, переносится в точку С2 непосредственно. При переносе в точку С2 силы P2 образуется пара (P2; -P2), отмеченная на рисунке тремя черточками.

2. Освободив вал в точках А и В от опор, заменяем действие опор их реакциями: подшипник А не препятствует горизонтальному смещению вала, поэтому его реакцию, расположенную в плоскости, перпендикулярной к оси вала, заменяем двумя составляющими: горизонтальной XA и вертикальной ZA; подпятник В препятствует смещению вала вдоль его оси, поэтому его реакцию заменяем тремя составляющими XB, YB и ZB (см рис. 169, б).

3. При известном навыке решения задач вместо расчетной схемы, показанной на рис. 169, б, можно получить более простую схему (рис. 169, в), на которой вместо пар сил круговыми стрелками обозначены их моменты. Так, круговой стрелкой M1 обозначен момент пары сил (P1; -P1), действующей в плоскости, перпендикулярной к оси у; M2 – момент пары (S1; -S1), действующей в плоскости, перпендикулярной к оси х, и M3 – момент пары (P2; -P2), действующей в плоскости, перпендикулярной к оси у.

Если силы выражать в кн, а плечи пар в м, то получим такие абсолютные числовые значения моментов M1 и M2:

Определение сил и реакций опор для редуктора с зубчатыми колесами