Решение задачи
1. Эта задача отличается от предыдущей тем, что в ней рассматривается движение не одной, а сразу двух материальных точек.
2. Изобразим перемещение обеих точек (рис. 199). Первая капля за искомое время t1 сек успевает пролететь расстояние s1 м. Вторая капля, начавшая падение через 0,5 сек, находится в падении t2=(t1-0,5) сек и успевает за это время пролететь расстояние s2 м.
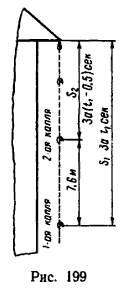
3. Расстояние 7,6 м между каплями через t1 сек после начала движения выразим в виде уравнения
(а) s1 - s2 = 7,6.
Используя формулу (5), получим уравнения падения капель:
для первой капли:
(б) s1 = 9,81*t12/2 ≈ 4,9t12;
для второй капли
(в) s2 = 9,81(t1 - 0,5)2/2 ≈ 4,9(t1 - 0,5)2.
4. Подставив в уравнение (а) значения s1 и s2 из уравнений (б) и (в), получаем уравнение, содержащее лишь одно неизвестное t1:
4,9t12 - 4,9(t1 - 0,5)2 = 7,6.
После раскрытия скобок и приведения подобных членов получим:
4,9t1 - 1,23 = 7,6,
откуда
t1 = (7,6 + 1,23)/4,9 = 1,8 сек.
Таким образом, через 1,8 сек после отрыва первой капли или через 1,8-0,5=1,3 сек после отрыва второй расстояние между ними будет составлять 7,6 м.