Решение задачи
1. На участке OA, длина которого 300 м, точка движется равноускоренно из состояния покоя и проходит этот участок за 30 сек:
sOA = 300 м, v0 = 0, tOA = 30 сек.
2. Находим ускорение aOA на участке OA из уравнения (5):
aOA = 2sOA/tOA2 = 2*300/302 = 2/3 м/сек2.
3. Скорость точки в конце участка OA находим из уравнения (6):
vA = aOAtOA = 2/3 * 30 = 20 м/сек.
4. Следующий участок траектории АВ длиной sAB=200 м точка проходит с постоянной скоростью vA=20 м/сек. Определяем время tAB, затраченное на это движение:
tAB = sAB/vA = 200/20 = 10 сек.
Причем в конце участка АВ скорость vB=vA=20 м/сек. Значит, движение на участке ВС точка начинает со скоростью vB=20 м/сек и, двигаясь равнозамедленно, останавливается в C (vC=0) через tBC=40 сек.
Длину участка ВС найдем по формуле (3), приняв s0=0:
sBC = (vB + vC)tBC/2 = (20 + 0)*40/2 = 400 м.
5. Ускорение aBC точки на участке ВС определяем из формулы (2):
aBC = (vC - vB)/tBC = (0 - 20)/40 = -0,5 м/сек2.
6. В конце траектории точка находится в покое в течение времени
tCC' = 20 сек.
7. Затем точка движется обратно и проходит равномерно путь
sCO = sCB + sBA + sAO = 400 + 200 + 300 = 900 м
за время tC'O = 30 сек.
Скорость точки в этом движении
vC'O = sCO/tC'O = 900/30 = 30 м/сек;
она направлена относительно скоростей первой части движения (например, относительно скоростей vA и vB) в обратную сторону.
8. На все движение точки по траектории ОАВС в одну и другую сторону вместе с остановкой в конце траектории С затрачено 130 сек, которые складываются из времени:
tOA = 30 сек – равноускоренного движения,
tAB = 10 сек – равномерного движения,
tBC = 40 сек – равнозамедленного движения,
tCC' = 20 сек – стояния точки,
tC'O = 30 сек – равномерного обратного движения.
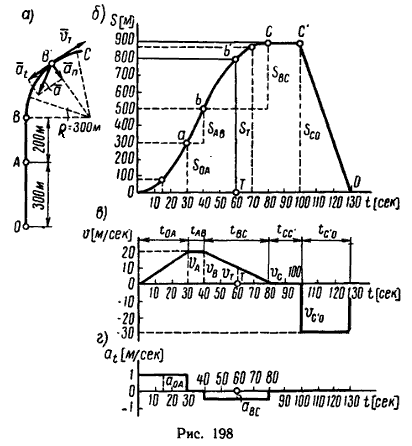
9. Описанное выше движение точки изображаем графически, построив три графика: перемещений, скоростей и ускорений, расположенных один под другим (рис. 198, б, в, г).
Для построения графиков необходимо выбрать удобные масштабы для времени и остальных величин.
Рекомендуется графики, показанные на рис. 198, вычертить самостоятельно на отдельном листе бумаги в клетку. Масштабы по оси времени на всех трех графиках одинаковы. Масштаб времени t принят равным μt≈2,9 сек/мм (2,9 сек в 1 мм) и поэтому на графике 130 сек изображаются отрезком, равным 45 мм. Масштаб перемещения s – μs=29 м/мм (29 м в 1 мм) и расстояние между началом траектории O и ее концом С, равное 900 м, изображается отрезком, равным 31 мм. Масштаб скоростей v – μv=2,86 м/(сек*мм) (2,86 м/сек в 1 мм) и 20 м/сек изображаются отрезком, равным 7 мм, а 30 м/сек – длиной 10 мм. Масштаб ускорений a – μa=0,25 м/(сек2*мм) (0,25 м/сек2 в 1 мм) и 1 м/сек2 изображается отрезком, равным 4 мм, а 0,5 м/сек2 – длиной 2 мм.
При самостоятельном построении этих графиков следует все масштабы увеличить, например принять
μt = 1 сек/мм; μs = 10 м/мм; μv = 1 м/(сек*мм) и μa=0,1 м/(сек2*мм).
10. После построения графиков определяем ускорение точки в момент времени T=60 сек после начала движения (см. условие задачи). Для этого прежде всего на графике перемещения из точки О (начало осей координат) по оси времени откладываем отрезок
OT = T/μt = 60 сек/2,9 сек/мм ≈ 21 мм.
Этот отрезок определит на оси времени время Т=60 сек (на самостоятельно построенном графике расстояние получится большим: 60 сек/1 сек/мм=60 мм).
Из точки Т восставим перпендикуляр Tb', измерив его, получим Tb'=28 мм, значит
sT = μs*Tb' = 29 м/мм * 28 мм ≈ 800 м.
Если это расстояние отложить на траектории, то увидим, что точка в момент времени T=60 сек будет находиться на криволинейном участке траектории (положение В') с радиусом кривизны R=300 м. Значит ускорение движущейся точки складывается из касательного at и нормального an ускорений.
Нормальное ускорение
an = vT2/R.
Скорость vT в момент времени Т=60 сек находим из графика скорости:
vT = μv*Tb' = 2,86 м/(сек*мм) * 3,5 мм ≈ 10 м/с.
Следовательно,
an = vT2/R = 102/300 = 1/3 м/сек2.
Касательное ускорение at находим из графика ускорений
at = aBC = -0,5 м/сек2.
Полное ускорение движущейся точки в момент времени Т=60 сек
a = sqrt(at2 + an2) = sqrt((1/2)2 + (1/3)2) ≈ 0,6 м/сек2.
Векторы vT, at, an и a, характеризующие кинематическое состояние точки в момент времени T=60 сек после начала движения, изображены на рис. 198, а.