Равномерное криволинейное движение точки

(Физика → Теоретическая механика → Кинематика точки → Задача 142)

Условие задачи

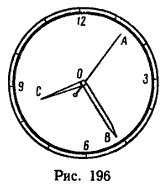
Определить, с какими скоростями движутся точки А, В и С, расположенные на концах секундной, минутной и часовой стрелок часов. Принять длину секундной и минутной стрелок равной 14 мм и длину часовой стрелки – 10 мм (рис. 196).

Рис. 196. Определить скорость стрелок часов

<< задача 141 || задача 146 >>

Решение задачи

1. Скорости данных точек найдем из формулы v = 2πr/T.

2. Определим исходные данные.

Для точки А (конец секундной стрелки)
OA = rA = 14 мм; TA = 1 мин = 60 сек.

Для точки В (конец минутной стрелки)
OB = rB = 14 мм; TB = 1 ч = 3600 сек.

Для точки С (конец часовой стрелки)
OC = rC = 10 мм; TC = 12 ч = 43200 сек.

3. Находим искомые скорости:
vA = 2πrA/TA = 2π*14/60 = 1,47 мм/сек;
vB = 2πrB/TB = 2π*14/3600 = 0,0244 мм/сек;
vC = 2πrC/TC = 2π*10/43200 = 0,00146 мм/сек.