Многоугольник сил. Определение равнодействующей сходящихся сил

(Физика → Теоретическая механика → Плоская система сходящихся сил → Задача 34)

Условие задачи

К концу В веревки АВ прикреплено кольцо, на которое действуют четыре силы: P1=40 н, P2=25 н, P3=25 н и P4=20 н, направленные, как показано на рис. 43, а (сила P2 горизонтальна). Определить усилие, возникшее в веревке, и ее направление относительно горизонтали.

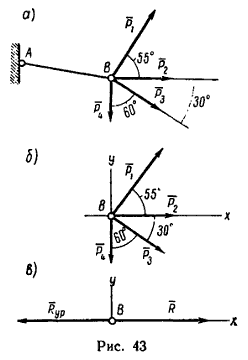
Рис. 43. К концу В веревки АВ прикреплено кольцо, на которое действуют четыре силы

<< задача 33 || задача 35 >>

Решение методом проекций

1. Веревка будет натянута равнодействующей четырех заданных сил. Следовательно, определив модуль равнодействующей, получим усилие, возникшее в веревке, а определив направление равнодействующей, найдем положение натянутой веревки.

2. Изобразим точку В с действующими на нее силами на отдельном рисунке (рис. 43, б) и совместим оси проекций с силами P2 и P4.

3. Найдем проекции заданных сил на ось х:
X1 = P1 cos 55° = 40 cos 55° = 22,9;
X2 = P2 = 25;
X3 = P3 cos 30° = 25 cos 30° = 21,6;
X4 = 0.

4. Находим проекции данных сил на ось у:
Y1 = P1 sin 55° = 40 sin 55° = 32,8;
Y2 = 0;
Y3 = -P3 sin 30° = -25 sin 30° = -12,5;
Y4 = -P4 = -20.

5. Найдем проекции равнодействующей R на оси х и у:
XR = 22,9 + 25 + 21,6 = 69,5;
YR = 32,8 - 12,5 - 20 = 0,3.

6. Найдем модуль равнодействующей:
R = sqrt(XR2 + YR2) = sqrt(69,52 + 0,32) = 69,5 н.

Как видно, в данном случае проекция равнодействующей на ось у очень мала по сравнению с проекцией на ось х. Поэтому равнодействующая практически численно равна проекции на ось х. Следовательно, можно принять, что вектор равнодействующей направлен вдоль оси х вправо (проекция на ось х положительна), т. е. горизонтально.

Таким образом, четыре заданные силы натягивают веревку равнодействующей силой R, приложенной к точке В (к кольцу на конце веревки) и направленной горизонтально.

Другой конец веревки (точка A, рис. 43, а) закреплен, поэтому на кольцо В со стороны веревки действует еще одна сила, численно равная равнодействующей, но направленная в противоположную сторону. Эта сила называется уравновешивающей системы четырех сил.

На рис. 43, в показаны равнодействующая R и уравновешивающая Rур.