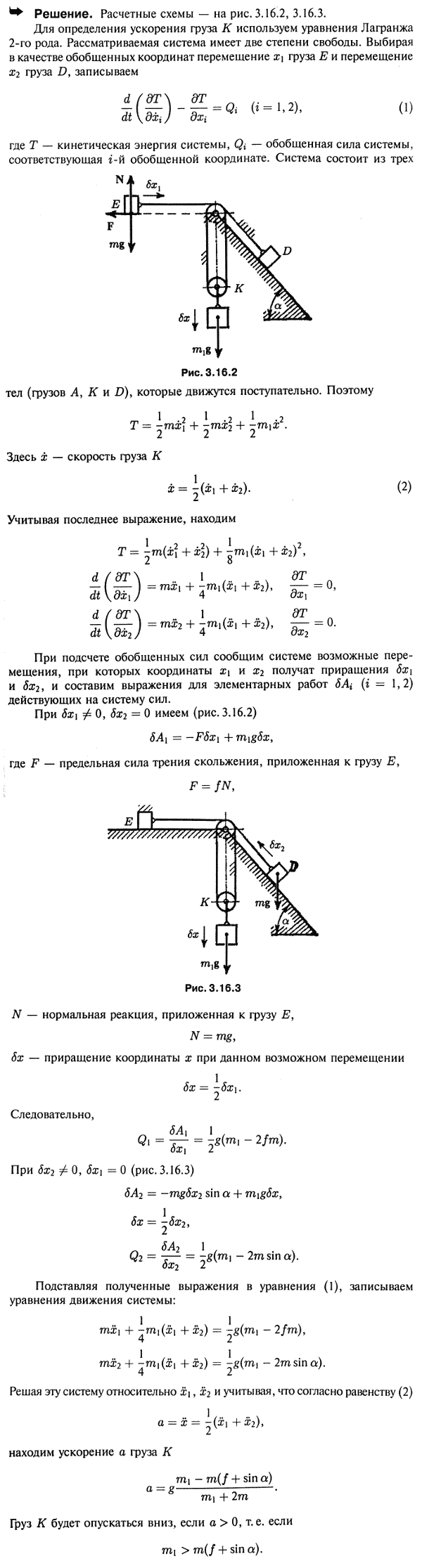
Решение задачи 48.27 из сборника Мещерского по теоретической механике

(Физика → Термех → Решебник Мещерского → Аналитическая механика → Уравнения Лагранжа 2-го рода)

Условие задачи

Два груза D и E массы m каждый привязаны к концам нерастяжимой нити. Эта нить от груза E идет через неподвижный блок A, затем охватывает подвижный блок B, возвращается вверх на неподвижный блок C, соосный с блоком A, проходит параллельно гладкой наклонной плоскости, где к концу нити привязан груз D. Наклонная плоскость образует угол α с горизонтом. К подвижному блоку B прикреплен груз K массы m₁. Коэффициент трения скольжения груза E о горизонтальную плоскость равен f. Массами блоков и нити пренебречь. Выяснить условие, при котором груз K будет опускаться. Найти ускорение этого груза. В начальный момент скорости всех грузов равнялись нулю.