Stanislav MM

Начинающий
|
      
547. найти площадь фигуры ограниченной линиями
г) У = ℮ ⁿ :У = ℮ ²ⁿ : Х = 1
при Х = 0 У = 1
М (0 : 1) это общая точка для двух кривых
Получаем две криволинейные трапеции.
Найдём площадь У = ℮ ²ⁿ
Для этого проинтегрируем ℮ ²ⁿ с верхним пределом 1, а нижним 0. Сначала найдём первообразную
℮ ²ⁿ = 1 / 2 • ℮ ²ⁿ
S ₁ = 1 / 2 • ℮ ² - ℮ ⁰ = 1 / 2 • ℮ ² - 1
Найдём площадь У = ℮ ⁿ
Первообразная ℮ ⁿ = ℮ ⁿ
S ₂ = ℮ ¹ - ℮ ⁰ = ℮ - 1
S = S ₁ - S ₂ = 1 / 2 • ℮ ² - 1 – (℮ - 1) = 1 / 2 • ℮ ² - 1 – ℮ + 1 = 1 / 2 • ℮ ² – ℮
Мой ответ S = 1 / 2 • ℮ ² – ℮
В книге S = 1 / 2 • ℮ ² – ℮ + 1 / 2
1 / 2 откуда взялась, или где я её потерял?
|
Всего сообщений: 82 | Присоединился: май 2012 | Отправлено: 3 июля 2012 17:27 | IP
|
|
Stanislav MM

Начинающий
|
      
Вернулся к изучению онлайн редактора.
На экране формула отображается на языке ЛАТАХ, а под экраном, в привычном для нас виде.
Вопрос:
Возможно ли увеличить экран?
Как скопировать на форум?
Внизу есть надпись «кликнуть здесь». её надо использовать?
|
Всего сообщений: 82 | Присоединился: май 2012 | Отправлено: 3 июля 2012 17:45 | IP
|
|
MEHT


Долгожитель
|
     
Цитата: Stanislav MM написал 3 июля 2012 11:52
Спасибо за проверку.
Онлайн редактор изучать не стал.
Причина:
Во - первых : мелкие символы. У меня дальнозоркость, поэтому я их не вижу. Газеты, журналы, книги – всё печатается мелким шрифтом. Поэтому если и читаю, то конкретную техническую литературу под хорошим освещением, с более сильными очками.
Во – вторых: Вы также сказали, что для этого надо немного знать язык ЛАТЕХ. Начал изучать информацию по данному вопросу.
Оказывается ЛАТЕХ – это международный язык и все научные и технические работы печатаются только на нём. Запомнить символы набора формул не сложно. Сначала наиболее употребляемые и простые. Потом более сложные. Мне установили программу Win Edt 6.0. Но я не знаю, как пошагово действовать от начала и до конца процесса. Набрал как написано в инструкции s5^2s. А как эту запись превратить в 5 ² ?
Какую кнопку надо нажать и где происходит превращение?
Плохо, что проблемы со зрением  У самого близорукость.. У самого близорукость..
Ну по крайней мере с ЛАТЕХом проще - весь его знать, разумеется, не обязательно. Да и программы-редакторы вроде Win Edt 6.0 Вам не понадобятся (если, конечно, не захотите глубоко познать искусство вёрстки ).
В самом онлайн-редакторе почти всё уже есть: основные конструкции кодов вынесены на лицевую панель сверху - достаточно кликнуть и нужная форма появится в окошке ввода - Вам останется только подставить в неё нужные числа или буквы (но только НЕ русские! - иначе формула не отобразится). А можно и вручную прописывать. Скажем, набрав в окошке
x^2 + y^2 = R^2
получите результат:
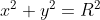
или набрав
\cos x = \frac{1}{2}
получите
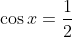
Также в правом верхнем углу прилагается ссылка (синий кружок с i) - это справка с примерами кодов и результатов их вёрстки в изображения. Очень полезная кстати.
Цитата: Stanislav MM написал 3 июля 2012 17:45
Вернулся к изучению онлайн редактора.
На экране формула отображается на языке ЛАТАХ, а под экраном, в привычном для нас виде.
Вопрос:
Возможно ли увеличить экран?
В браузере попробуйте увеличить масштаб со 100% до 200% или больше - картинка увеличится..
В Internet_Explorer - правый нижний угол экрана (там будет доступен список масшабов при клике).
В Опере - также в правом нижнем углу есть плавный регулятор масштаба, а можно пользоваться горячими клавишами "+" и "-".
Или же в обоих браузерах в строке меню: "Вид" -> "Масштаб" -> ...
Цитата: Stanislav MM написал 3 июля 2012 17:45
Как скопировать на форум?
Внизу есть надпись «кликнуть здесь». её надо использовать?
Кликнув по ссылке Вы тем самым сможете загрузить картинку-формулу себе на жесткий диск.
А нам нужна только ссылка на эту картинку для последующей вставки на форум.
Вот тут снова встаёт вопрос - каким браузером Вы пользуетесь?
Если оперой, то кликаете правой кнопкой мышки по картинке с формулой - в выплывающем меню выбираете "Копировать адрес изображения" - ссылка на картинку скопируется в буфер. После - вставляете её в поле набора текста форума, окружив тэгами [img ] [/img ] для отображения картинки.
В Internet_Explorer такой опции нет, но есть вариант кликнув по картинке прав. кнопкой мышки перейти в "Свойства" и там в окошке справа от "Адрес (URL)" кликаете правой кнопкой мышки по ссылке - "Выделить всё", а потом также и "Копировать" - нужная ссылка будет скопирована в буфер. Её вставляете на форум (так же как и абзацем выше).
Через другие браузеры, думаю, будет аналогично. Во всяком случае через "свойства" всегда можно получить ссылку на нашу картинку-формулу.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 4 июля 2012 2:11 | IP
|
|
MEHT


Долгожитель
|
     
Цитата: Stanislav MM написал 3 июля 2012 17:27
547. найти площадь фигуры ограниченной линиями
г) У = ℮ ⁿ :У = ℮ ²ⁿ : Х = 1
при Х = 0 У = 1
М (0 : 1) это общая точка для двух кривых
Получаем две криволинейные трапеции.
Найдём площадь У = ℮ ²ⁿ
Для этого проинтегрируем ℮ ²ⁿ с верхним пределом 1, а нижним 0. Сначала найдём первообразную
℮ ²ⁿ = 1 / 2 • ℮ ²ⁿ
S ₁ = 1 / 2 • ℮ ² - ℮ ⁰ = 1 / 2 • ℮ ² - 1
Найдём площадь У = ℮ ⁿ
Первообразная ℮ ⁿ = ℮ ⁿ
S ₂ = ℮ ¹ - ℮ ⁰ = ℮ - 1
S = S ₁ - S ₂ = 1 / 2 • ℮ ² - 1 – (℮ - 1) = 1 / 2 • ℮ ² - 1 – ℮ + 1 = 1 / 2 • ℮ ² – ℮
Мой ответ S = 1 / 2 • ℮ ² – ℮
В книге S = 1 / 2 • ℮ ² – ℮ + 1 / 2
1 / 2 откуда взялась, или где я её потерял?
У Вас первая первообразная имеет вид 1/2 • ℮ ²ⁿ , следовательно площадь должна быть разностью первообразных
S ₁ = 1/2 • ℮ ² - 1/2 • ℮ ⁰ = 1/2 • (℮ ² - 1).
А у Вас потерян коэффициент 1/2 у вычитаемой экспоненты.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 4 июля 2012 2:16 | IP
|
|
Stanislav MM

Начинающий
|
      
Большое спасибо за помощь.
В примере Вы хорошо объяснили, где была потеряна 1 / 2.
Масштаб в онлайн редакторе увеличил.
Не понял, как делать многоэтажные дроби и начинать с новой строки. Онлайн редактор – хорошая штука, в том числе с точки зрения изучения языка ЛАТЕХа.
Я пользуюсь браузером Мозило. После нажатия правой кнопки мыши появилось «копировать изображение» и «копировать ссылку на изображение». Выбрал второе. Перешел на форум.
Надпись вставить стала активной.
В онлайн редактор было набрано 1 / sin x .
Вся это абракадабра скопировалось, окружил тегами [img][/img]. но на форум не пошла ни в каком виде.
|
Всего сообщений: 82 | Присоединился: май 2012 | Отправлено: 4 июля 2012 11:15 | IP
|
|
Stanislav MM

Начинающий
|
      

|
Всего сообщений: 82 | Присоединился: май 2012 | Отправлено: 4 июля 2012 11:22 | IP
|
|
MEHT


Долгожитель
|
     
Так Вы пробовали отправлять?
Ссылка правильная, всё должно отобразится.
Разве ж что, стоит проследить за её целостностью при вставке (не должно быть обрывов).
Что ещё можно сказать.. в самом онлайн-редакторе чуть ниже основного окна ввода есть настройки шрифта и размера. Вы можете оставить по-умолчанию: (10pt) Нормальный, 110.
Сама ссылка тогда будет сразу начинатся с кода-формулы после слов
...gif.latex?
минуя команды \large и \dpi{} - по сути ответственные за размеры формулы; т.е. будет выглядеть так:
внешняя ссылка удалена
Заключаете её в тэги [img ][/img ] и отправляете - картинка будет отображена в сообщении.
---
Многоэтажные дроби делаются путём многократных вложений друг в друга кода \frac{}{}.
Пример: \frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{2}}}} даёт
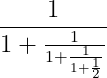
(я увеличил масштаб картинки со 110 до 150)
Посмотрите справку, там множество примеров.
Перейти на новую строку - двойной обратный слэш: \\
Примечательно, что первая строка формулы будет при этом иметь отступ в отличие от последующих строк. Чтобы его убрать, \\ следует ставить в начале первой строки перед непосредственным набором кодов-формул.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 5 июля 2012 2:41 | IP
|
|
Stanislav MM

Начинающий
|
      
Цитата: MEHT написал 3 июля 2012 3:48
Цитата: Stanislav MM написал 20 июня 2012 13:11
В этой книге есть формула первообразной если число стоит в числителе. А если число стоит в знаменателе, то такой формулы нет. Не сразу понял, что это имеет значение. Глядя на решённые примеры я понял как она выглядит F(x) = - (n -1) • Х ⁿ⁻¹.
Пример который я привёл первый и самый простой в теме первообразные. Если его не решить в ручном режиме, и не понять, как это находится, то дальше я не решу ни одного примера по нахождению первообразной тригонометрической функции.
Спасибо за любую конкретную информацию.
Вы спрашиваете про первообразные от
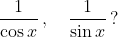
|
Всего сообщений: 82 | Присоединился: май 2012 | Отправлено: 5 июля 2012 12:30 | IP
|
|
Stanislav MM

Начинающий
|
      
Да, я не очень понимаю и первообразные и производные тригонометрических функций.
Поэтому, во всех темах не решаю примеры с тригонометрическими функциями.
Пример: найти производную sin 2x. Нет ни формулы ни примеров решения в книге .
От Вас узнал, что это будет 2 sin 2x . Потом проверил МАТКАДом – тот же результат. А какая производная будет у sin ² x , sin x ² ?
Пробовал решать, но мои ответы и ответы в книге – это две разные вещи.
Дойду по темам до конца книги, а потом начну решать с начала, примеры с тригонометрическими функциями.
Как Вы вставляете цитаты? Нажимаю на эмблему «цитата», а копируется всё сообщение. Выделяешь нужное место, а копируется всё собщение.
|
Всего сообщений: 82 | Присоединился: май 2012 | Отправлено: 5 июля 2012 12:35 | IP
|
|
MEHT


Долгожитель
|
     
Да, я не очень понимаю и первообразные и производные тригонометрических функций.
Поэтому, во всех темах не решаю примеры с тригонометрическими функциями.
Сложного тут ничего нет. Всё, от чего изначально следует отталкиватся при получении табличных производных от синуса или косинуса - это первый замечательный предел.
Далее, например, уже из одного
'=%5Ccos%20x)
можно получить табличные
'=-%5Csin%20x)
и
'=%5Cfrac{1}{%5Ccos^2x}=1+%5Ctextrm{tg}^2%20%5C,x)
пользуясь при этом только правилами дифференцирования и тригонометрическими тождествами (в первом - представив косинус через синус со смещённым на пи/2 аргументом, во втором - дифференцирование частного).
А какая производная будет у sin ² x , sin x ² ?
Так sin ² x и (sin x)² - это одно и то же,
просто в первом случае более удобно записан квадрат синуса.
Различие будет, если квадрат относится к x: в смысле sin(x² ).
Если так, то в обоих случаях дифференцируете как сложную функцию:
(sin ² x)' = 2∙sin(x) ∙ cos(x) = sin(2x),
(sin(x² ))' = cos(x² ) ∙ 2x.
Как Вы вставляете цитаты? Нажимаю на эмблему «цитата», а копируется всё сообщение. Выделяешь нужное место, а копируется всё собщение.
К сожалению этот форум не поддерживает частичного цитирования. Приходится либо цитировать полностью, а после вручную удалять лишнее, оставляя только цитируемое,
либо копировать цитируемый текст и окружать его тэгами [quote ] [/quote ].
(Сообщение отредактировал MEHT 7 июля 2012 7:44)
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 7 июля 2012 7:43 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.1.6 Первообразная (неопределенный интеграл)
2.1.6 Первообразная (неопределенный интеграл)

 Форум
Форум

 Математика
Математика

 2.1.6 Первообразная (неопределенный интеграл)
2.1.6 Первообразная (неопределенный интеграл)