Форум - 2.1.6 Первообразная (неопределенный интеграл) [56]

Форум	» Назад на решение задач по физике и термеху
Регистрация \| Профиль \| Войти \| Забытый пароль \| Присутствующие \| Справка \| Поиск

» Добро пожаловать, Гость: Войти | Регистрация

	Форум Математика 2.1.6 Первообразная (неопределенный интеграл)
	Отметить все сообщения как прочитанные [ Помощь ] » Добро пожаловать на форум "Математика" «

Переход к теме
<< Назад Вперед >>

Несколько страниц [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 ]
Модераторы: Roman Osipov, RKI, attention, paradise

MEHT

Долгожитель

Цитата: sharm написал 22 апр. 2012 13:13
ситуация такая:
есть интеграл: (xdx)/((3-2x-x^2)^1/2), кjторый я взял и получилась первообразная: -(3-x^2-2x)^1/2 - sin^-1(1/2*(x+1))+c

Не будет там ни синусов, ни арксинусов. Интеграл взят неверно.

Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 24 апр. 2012 18:21 | IP

MEHT

Долгожитель
optimus, универсальная тригонометрическая замена t=tg(x/2)

Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 24 апр. 2012 18:25 | IP

Gaechka

Новичок
Здравствуйте!
Уже не первый день бьюсь с интегралом. Помогите пожалуйста! Пробовала делать замену переменной, но этим только усложнялась задача, интегрирование по частям тоже не привело к результату.
интеграл: (sqrt(9+x^2)/(x^2+1))dx

Всего сообщений: 5 | Присоединился: апрель 2012 | Отправлено: 25 апр. 2012 0:21 | IP

MEHT

Долгожитель
Ну, Вы всегда можете воспользоваться подстановками Эйлера. Для рациональных интегралов, содержащих радикалы от квадратных трёхчленов, это универсальный метод.
В частности, можно взять подстановку

$\xi = x+\sqrt{x^2+9}$

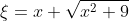
откуда

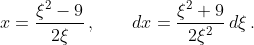
$x=\frac{\xi^2-9}{2\xi}\,, \qquad dx=\frac{\xi^2+9}{2\xi^2}\,d\xi\,.$

Ваш интеграл представится уже рациональным выражением без радикалов

$\int{\frac{\xi - \frac{\xi^2-9}{2\xi} }{\left ( \frac{\xi^2-9}{2\xi} \right )^2+1}\cdot \frac{\xi^2+9}{2\xi^2}\,d\xi} = \\\\\\ =\int {\frac{\left ( \xi^2+9 \right )^2 d\xi }{\left [\left ( \xi^2-9 \right )^2+4\xi^2 \right ]\xi }}$

в котором можно пораскрывать все скобки и разбивать подынтегральное на элементарные дроби.
А можно немножко упростить выкладки, домножив числитель и знаменатель на 2ξ. Внеся это 2ξ в числителе под дифференциал
2ξ dξ = d(ξ² ) получите интеграл, где всюду фигурируют только ξ² и интегрируется по ξ².

Но я хочу показать и другой способ. Он поизящней и без многоэтажных дробей.

Применяем замену x = 3*sh(t) в результате которой

$\int{\frac{\sqrt{x^2+9}}{x^2+1}\,dx} = \int{\frac{9\, \textrm{ch}^2t}{9\, \textrm{sh}^2t+1}\,dt} = \int{\frac{9\, \textrm{ch}^2t}{9\, \textrm{ch}^2t-8}\,dt}=\\\\\\ = \int{\left (1+\frac{8}{9\, \textrm{ch}^2t-8} \right )dt} = \int dt \,+\, \int{\frac{8}{9-8\left ( 1-\textrm{th}^2t \right )} \, \frac{\,dt}{\textrm{ch}^2t}} =\\\\\\ = \int dt \,+\,\int{\frac{8\,d\left (\textrm{th}\,t \right )}{1+8\,\textrm{th}^2t}} = \int dt \,+\,\int{\frac{\,d\left (\textrm{th}\,t \right )}{ \left (\frac{1}{\sqrt{8}} \right )^2 + \,\textrm{th}^2t}} =\\\\ = t + \sqrt{8} \ \textrm{arctg}\left ( \sqrt{8}\ \textrm{th}\,t \right ) +C\, .$

Теперь осталось вернутся назад к иксу.

$\textrm{arcsh}\left ( \frac{x}{3} \right ) + \sqrt{8} \ \textrm{arctg}\left ( \sqrt{8}\ \frac{x}{\sqrt{x^2+9}} \right ) +C\,$

Арксинус гиперболический - иначе "длинный логарифм"

$\textrm{arcsh}\,x = \ln\left ( x+\sqrt{x^2+1} \right )$

Можно оставить ответ как есть, можно переписать через этот логарифм. И то, и это будет уже будет ответом.
Через логарфим:

$\ln\left ( x+\sqrt{x^2+9} \right ) - \ln3 + \sqrt{8} \ \textrm{arctg}\left ( \sqrt{8}\ \frac{x}{\sqrt{x^2+9}} \right ) +C\,$

логарифм тройки можно вычеркнуть - сказать, что входит в константу С.

Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 25 апр. 2012 14:26 | IP

Gaechka

Новичок
МЕНТ, спасибо Вам преогромнейшее!!!

Всего сообщений: 5 | Присоединился: апрель 2012 | Отправлено: 25 апр. 2012 18:20 | IP

sharm

Новичок

Цитата: MEHT написал 24 апр. 2012 18:21
Цитата: sharm написал 22 апр. 2012 13:13
ситуация такая:
есть интеграл: (xdx)/((3-2x-x^2)^1/2), кjторый я взял и получилась первообразная: -(3-x^2-2x)^1/2 - sin^-1(1/2*(x+1))+c

Не будет там ни синусов, ни арксинусов. Интеграл взят неверно.

Я конечно извиняюсь, но все верно взято, сегодня на консультации подтвердилось и с профессором разобрано, просто ступил и к выражению
arcsin(1/2*(x{1))
не внимательно отнесся
если интересует могу выложить снимок с решения

Всего сообщений: 20 | Присоединился: декабрь 2011 | Отправлено: 25 апр. 2012 19:50 | IP

MEHT

Долгожитель
Это я извиняюсь, конечно же Вы правы. Правильно так

$\int{\frac {x\,dx}{\sqrt{3-2x-x^2}}}=\int{\frac{x\,dx}{\sqrt{4-(x+1)^2}}}= \int{\frac {d(x^2 )}{2\sqrt{4-(x+1)^2}}}=\\\\\\ =-\int{\frac {d [ 4-( x+1 )^2 + {\color{Red}2(x+1)} ]}{2\sqrt{4-(x+1)^2}}}= -\int{\frac {d[4-(x+1)^2]}{2\sqrt{4-(x+1)^2}}}\,- \int{\frac {d(x+1)}{\sqrt{4-(x+1)^2}}}=\\\\ =-\sqrt{4-(x+1)^2} \ - \textrm{arcsin}\left ( \frac{x+1}{2} \right )+C.$

Это я в уме неверно внёс под дифференциал, забыл про 2(x+1).
---
Проверка дифференцированием - это по сути чтение равенства интегрирования справа налево.. конечно, если не делать замены переменной

Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 25 апр. 2012 21:19 | IP

Lavavoth

Новичок
del

(Сообщение отредактировал Lavavoth 21 мая 2012 14:20)

Всего сообщений: 3 | Присоединился: апрель 2012 | Отправлено: 30 апр. 2012 14:02 | IP

MEHT

Долгожитель
Посмотрите как топик раскорячило от Ваших полотнищ!
Через внешняя ссылка удалена было бы куда удачней.

Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 1 мая 2012 16:57 | IP

lyntic12345

Новичок
помогите пожалуйста решить
1) интеграл х* 2^-х
2) интеграл X * sin x/ cos^ 2 x

Всего сообщений: 1 | Присоединился: май 2012 | Отправлено: 9 мая 2012 9:24 | IP

Отправка ответа:

Имя пользователя Вы зарегистрировались?
Пароль Забыли пароль?
Сообщение
Использование HTML запрещено
Использование IkonCode разрешено
Смайлики разрешены

Опции отправки
Добавить подпись?
Получать ответы по e-mail?
Разрешить смайлики в этом сообщении?
Просмотреть сообщение перед отправкой? Да Нет

Переход к теме
<< Назад Вперед >> Несколько страниц [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 ]