Latisha


Новичок
|
     
Помогите, пожалуйста, решить:
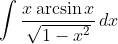
(Сообщение отредактировал attention 22 марта 2010 14:26)
|
Всего сообщений: 5 | Присоединился: март 2010 | Отправлено: 22 марта 2010 0:12 | IP
|
|
attention 


Долгожитель
|
      
Цитата: Latisha написал 22 марта 2010 0:12
Помогите, пожалуйста, решить:
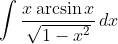
Используйте интегрирование по частям:
 = \hfill \\ = - \sqrt{1 - x^2}\,\arcsin{x}+ \int\sqrt{1 - x^2}\,d(\arcsin{x}) = \hfill \\ = - \sqrt{1 - x^2}\,\arcsin{x}+ \int{dx} = \hfill \\ = x - \sqrt{1 - x^2}\,\arcsin{x}+ C. \hfill\\\end{gathered})
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 22 марта 2010 14:28 | IP
|
|
attention 


Долгожитель
|
      
Цитата: compas написал 21 марта 2010 13:59
спасибо, за предыдущий интеграл, если не трудно, могли бы с этим помочь


(Сообщение отредактировал attention 22 марта 2010 14:43)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 22 марта 2010 14:42 | IP
|
|
Latisha


Новичок
|
     
Спасибо огромное, attention!!!! =***
|
Всего сообщений: 5 | Присоединился: март 2010 | Отправлено: 23 марта 2010 2:10 | IP
|
|
Latisha


Новичок
|
     
Ребят, помогите, пожалуйста.... Не получается решить=(я запуталась.
int(x^3-8x^2)^(1/3)dx
и вот этот еще...
int(3x-4)/(x^2-4)dx
|
Всего сообщений: 5 | Присоединился: март 2010 | Отправлено: 28 марта 2010 22:58 | IP
|
|
Olegmath2

Полноправный участник
|
      
Цитата: Latisha написал 28 марта 2010 22:58
Ребят, помогите, пожалуйста.... Не получается решить=(я запуталась.
int(x^3-8x^2)^(1/3)dx
и вот этот еще...
int(3x-4)/(x^2-4)dx
1) I=int (x^2*(x-8))^(1/3)dx=int x^(2/3)*(x-8)^(1/3)dx.
Имеем интеграл от дифференциального бинома, т.е. интеграл вида
int x^m*(a+bx^n)^p*dx. Поскольку p=r/s=1/3 – нецелое число, (m+1)/n+p=(2/3+1)/1+1/3=2 – целое число, то с помощью третей подстановки Чебышёва: a+bx^n=(t^s)*x^n, где t – новая переменная, данный интеграл приводится к интегралу от рациональной функции. В данном случае подстановка будет такой: x-8=(t^3)*x.
2) Применяя свойства неопределённого интеграла получаем, что исходный интеграл I сводится к вычислению двух интегралов I1 и I2
I= int(3x-4)/(x^2-4)dx = 3*int (x*dx)/(x^2-4) – 4* int dx/(x^2-4)=3*I1-4*I2.
Интеграл I1 вычисляется с помощью замены переменной: t=x^2-4, а второй интеграл I2 является табличным.
(Сообщение отредактировал Olegmath2 30 марта 2010 0:16)
|
Всего сообщений: 235 | Присоединился: февраль 2009 | Отправлено: 29 марта 2010 2:11 | IP
|
|
TinkyVinky

Новичок
|
     
Помогите, пожалуйста...
int((tgx)^(1/2))/sin2x*dx
int(4x+x^2)^(1/2)*dx
Заранее огромное спасибо!
|
Всего сообщений: 4 | Присоединился: март 2010 | Отправлено: 29 марта 2010 16:11 | IP
|
|
Latisha


Новичок
|
     
Olegmath2, спасибо большое. Второй дорешала, а вот с первым всё никак не справлюсь.
|
Всего сообщений: 5 | Присоединился: март 2010 | Отправлено: 29 марта 2010 21:28 | IP
|
|
Latisha


Новичок
|
     
Справилась))
|
Всего сообщений: 5 | Присоединился: март 2010 | Отправлено: 31 марта 2010 17:26 | IP
|
|
franca


Новичок
|
      
Доброго времени суток,помогите пожалуйста решить:
int((arccosx)^3-1)/(1-x^2)^1/2*dx
|
Всего сообщений: 1 | Присоединился: апрель 2010 | Отправлено: 1 апр. 2010 15:35 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.6 Первообразная (неопределенный интеграл)
2.1.6 Первообразная (неопределенный интеграл)

 Форум
Форум

 Математика
Математика

 2.1.6 Первообразная (неопределенный интеграл)
2.1.6 Первообразная (неопределенный интеграл)