Gumir

Новичок
|
      
вот ещё несколько задачек=)
3. найти вероятность попадания в заданный интервал (a,b) нормально расспределеной случайной величины Х. если известны её математическое ожидание m и среднее квадратическое отклонение d. Написать выражение плотности распределения вероятнотсти случайной величины Х. a=1, b= 5, m= 4, d= 1
|
Всего сообщений: 3 | Присоединился: март 2011 | Отправлено: 4 марта 2011 16:42 | IP
|
|
Gumir

Новичок
|
      
4. Известно, что дисперсия каждой из данных независимых случайных величин не превышает 4. Определить число таких величин, при котором вероятность отклонения средней арифметической случайных величин от средней арифметической их математических ожиданий не более чем на 0,25 превысит 0,99
|
Всего сообщений: 3 | Присоединился: март 2011 | Отправлено: 4 марта 2011 16:48 | IP
|
|
Lyuda

Начинающий
|
      
Непрерывная случайная величина X задана законом распределения
f(x)= 0, x<0 или с(1+x^2), 0<x=<1>1;
Найти: 1) коэффициент C; 2) функцию распределения F(x); 3) математическое
f(x)= 0, при x<0
f(x)= с(1+x^2),при 0<=x=<1
f(x)=0 при x>1;
Решение
1) dx=1 )
dx=c(x+\frac{x^3}{3})|_0^1=c(1+\frac{1}{3})=c\frac{4}{3}=1 )

f(x)= 0, при x<0
f(x)= 3/4(1+x^2),при 0<=x=<1
f(x)=0 при x>1;
2)
=\int\limits_{-\infty}^xf(x)dx )
=\int_{-\infty}^x0dx=0 )
=\int\limits_{-\infty}^00dx+\int\limits_{0}^x\frac{3}{4}(1+x^2)dx=0+\frac{3}{4}(x+\frac{x^3}{3})|_0^x=\frac{3}{4}(x+\frac{x^3}{3}) )

=\int\limits_{-\infty}^00dx+\int_{0}^1\frac{3}{4}(1+x^2)dx+\int\limits_{0}^x0dx=0+\frac{3}{4}(x+\frac{x^3}{3})|_0^1=\frac{3}{4}(1+\frac{1^3}{3})=\frac{3}{4}\frac{4}{3}=1 )
F(x)=0 при x<0
= \frac{3}{4}(x+\frac{x^3}{3}),\qquad <br>0\leq x\leq 1;)
F(x)=1 при x>1
3) 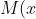=\int\limits_0^1xf(x)dx=\int\limits_0^1x\frac{3}{4}(1+x^2)dx=\frac{3}{4}\int\limits_0^1(x+x^3)dx=\frac{3}{4}(\frac{x^2}{2}+\frac{x^4}{4})|_0^1=\frac{3}{4}(\frac{1}{2}+\frac{1}{4})\frac{3}{4}+\frac{3}{4}=1,5. )
|
Всего сообщений: 73 | Присоединился: ноябрь 2007 | Отправлено: 4 марта 2011 18:00 | IP
|
|
Kitsune

Новичок
|
     
В продажу поступают телевизоры 3 заводов. Продукция первого завода содержит 20% телевизоров со скрытным дефектом, второго- 10%, третьего - 5%. Какова вероятность приобрести исправный телевизор, если в магазин поступило 30% с первого завода, 20%-со второго завода и 50% - с третьего?
Помогите пожалуйста.))) За ранее спасибо)))
|
Всего сообщений: 22 | Присоединился: декабрь 2010 | Отправлено: 5 марта 2011 7:07 | IP
|
|
Besna


Начинающий
|
     
Alisa
Вероятность того, что .....Вероятность того, что случайно выбран
Как я полагаю найти Р, что случайно выбранный клиент банка не вернет заем.
Решение:
Применяем формулу Бейса:
А = (клиент банка не вернет заем)
H1 = (период экономического роста)
H2 = (период экономического кризиса)
Р(Н1) = 0,65; Р(Н2) = 0,35; Р(А/Н1) = 0,04; Р(А/Н2) = 0,13;
Р(А) = 0,65* 0,04 + 0,35* 0,13= 0,0715
Р(Н1/А) = 0,65*0,04/0,715 = 0,365 - Р что клиент не вернёт заём.
|
Всего сообщений: 61 | Присоединился: февраль 2011 | Отправлено: 5 марта 2011 18:40 | IP
|
|
Kitsune

Новичок
|
     
В продажу поступают телевизоры 3 заводов. Продукция первого завода содержит 20% телевизоров со скрытным дефектом, второго- 10%, третьего - 5%. Какова вероятность приобрести исправный телевизор, если в магазин поступило 30% с первого завода, 20%-со второго завода и 50% - с третьего?
помогите.....пожалуйста))
|
Всего сообщений: 22 | Присоединился: декабрь 2010 | Отправлено: 7 марта 2011 8:44 | IP
|
|
Besna


Начинающий
|
     
Kitsune
... Какова вероятность приобрести исправный телевизор?
Задача решается по формуле Полной вероятности.
|
Всего сообщений: 61 | Присоединился: февраль 2011 | Отправлено: 7 марта 2011 9:10 | IP
|
|
Kitsune

Новичок
|
     
Цитата: Besna написал 7 марта 2011 9:10
Kitsune
... Какова вероятность приобрести исправный телевизор?
Задача решается по формуле Полной вероятности.
Простите я проболела эту тему, а преподаватель не объяснит а так я не пойму, можете объяснить???
|
Всего сообщений: 22 | Присоединился: декабрь 2010 | Отправлено: 7 марта 2011 9:32 | IP
|
|
Besna


Начинающий
|
     
А = {купили испр TV}; Нn - {TV поступил в продажу}
Р(Н1)=0.3 - поступило с 1ого завода. Р(Н2)=0.2 - ... 2ого, Р(Н3)=0.5 - ...3еог.
Р(А/Н1)=0.8 - поступило без дефекта с 1ого заврда. Р(А/Н2)=0.2, Р(А/Н2)=0.9. Р(А/Н3)=0.95.
Р(А)=Р(Н1)*Р(А/Н1)+Р(Н2)*Р(А/Н2)+Р(Н3)*Р(А/Н3)=
|
Всего сообщений: 61 | Присоединился: февраль 2011 | Отправлено: 7 марта 2011 9:48 | IP
|
|
Kitsune

Новичок
|
     
спасибо за помощь)))
|
Всего сообщений: 22 | Присоединился: декабрь 2010 | Отправлено: 7 марта 2011 9:59 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.6.2(2) Теория вероятностей в примерах
2.6.2(2) Теория вероятностей в примерах

 Форум
Форум

 Математика
Математика

 2.6.2(2) Теория вероятностей в примерах
2.6.2(2) Теория вероятностей в примерах