Sokratus


Долгожитель
|
      
График возьмите из любого учебника по микроэкономике. Это простая модель спроса и предложения. Равновесие в ней - это точка пересечения кривых, т.е. равенство объемов спроса и предложения (Qd = Qs). Найденную равновесную цену Ре подставляете в любое из уравнений и находите равновесный объем Qе. Выручка TR - это произведение цены на количество.
|
Всего сообщений: 599 | Присоединился: декабрь 2008 | Отправлено: 16 дек. 2011 0:59 | IP
|
|
Jonik


Новичок
|
     
Сократус ответьте пожалуйста.
|
Всего сообщений: 14 | Присоединился: декабрь 2011 | Отправлено: 16 дек. 2011 1:05 | IP
|
|
Jonik


Новичок
|
     
Функция спроса на пшеницу имеет вид Qd-8000-20•P, где Qd - внличина спроса на пшеницу в тоннах,
а P - цена пшеницы в ден. ед. за тонну. предложение пшеницы на рынке описывается функцией
Qs=30•P-600, где Qs - величина предложения пшеницы в тоннах, а P - цена пшеницы в ден. ед. за тонну.
Государство установило нижний уровень цены ("пол цены") равный 200 ден. ед. за тонну.
1) Какая ситуация сложится на рынке - дефицит или затоваривание? Обьясните почему.
2) Как и на сколько изменится выручка продавцов пшеницы по сравнению с ситуацией нерегулируемого рынка?
3) Ответ проиллюстрируйте с помощью графиков спроса и предложения.
|
Всего сообщений: 14 | Присоединился: декабрь 2011 | Отправлено: 16 дек. 2011 1:36 | IP
|
|
Sokratus


Долгожитель
|
      
1) Подставим цену в обе функции: Qd = 8000 - 20*200 = 4000 т., Qs = 30*200 - 600 = 5400 т. Т.к. Qd < Qs, то на рынке будет наблюдаться затоваривание величиной 5400 - 4000 = 1400 т.
2) Найдем координаты точки рыночного равновесия при Qd = Qs:
8000 - 20P = 30P - 600; 50P = 8600; Pe = 172 ден. ед.; Qe = 4560 т.
Выручка в точке равновесия равна TR = PeQe = 172*4560 = 784320 ден. ед. Выручка при цене пола составляет TR` = Pf*Qd = 200*4000 = 800000 ден. ед. Следовательно, выручка сократится на 800000 - 784320 = 15680 ден. ед.
3)
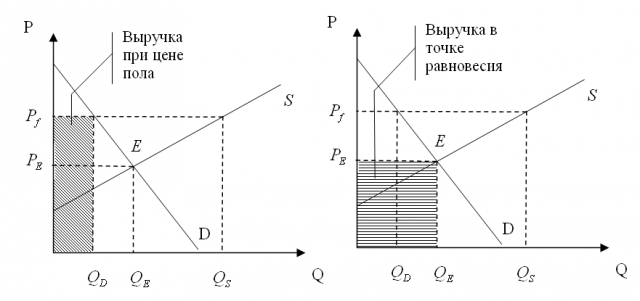
|
Всего сообщений: 599 | Присоединился: декабрь 2008 | Отправлено: 16 дек. 2011 19:30 | IP
|
|
Jonik


Новичок
|
     
1) Издержки фирмы заданы функцией TC=0,5Q²+Q+6, а цена на её продукцию не зависит от объёма выпуска и равна 100 ден. ед. Определите выпуск, при котором прибыль фирмы максимальна и величину этой прибыли. По возможности описать ход решения.
2) На рынке совершённой конкуренции рыночный спрос задан функцией Q=50-P, а предложение выражается функцией Q=-10+2P. Функция общих издержек каждой фирмы, работающей на этом рынке, задаётся TC=5Q²+10Q.
Определите: а) объём производства одной фирмы, при котором её прибыль максимальна и величину этой прибыли.
б) Количество фирм на рынке.
Государство установило максимальный уровень цены, равный 15 ден. ед.
в) объём производства одной фирмы, при котором её прибыль максимальна и величину этой прибыли при новой цене.
г) как измениться количество фирм на рынке? По возможности описать ход решения.
3) Сельскохозяйственная фирма, действующая на рынке совершенной конкеренции, максимизирует прибыль, выращивая 12 тонн кукурузы в год. Определите рыночную цену тонны кукурузы, если функция издержек фирмы имеет вид TC=2Q²+3Q. По возможности описать ход решения.
|
Всего сообщений: 14 | Присоединился: декабрь 2011 | Отправлено: 16 дек. 2011 22:40 | IP
|
|
Skyrazor


Новичок
|
     
Доброго времени суток знатокам) Помогаю знакомой, две задачи. Сам что-то наклепал при помощи Интернета, проверьте пожалуйста, и, если неверно, будьте так добры, поправьте меня.
I. Фирма действует на конкурентном рынке. Функция общих издержек производства имеет вид TC = 100 + Q^2; MC = 2Q; FC = 100 дол.
1) Если цена единицы товара равна 60 дол., то сколько нужно произвести товаров, чтобы максимизировать прибыль?
2) Чему равен объём этой прибыли?
3) Каков минимальный уровень рыночной цены, до которого фирма будет продолжать производство?
II. Функция общих издержек конкурентной фирмы в долгосрочном периоде имеет вид TC = 2400Q - 10Q + 5Q^3. Определите уровень равновесной цены продукта фирмы в долгосрочном периоде.
А теперь мои решения:
I. 1) MR = P = 60; MC = MR = 60; 60 = 2Q; Q = 30;
2) Объём прибыли: 60*30 = 1800
3) P = AVC; AVC = VC/Q; VC = 2Q + Q^2; AVC = (2Q + Q^2)/Q = 2 + Q; AVC = 2 + 30 = 32
II. P = LMC = LAC.
LMC = (TC)' = 240 - 20Q + 15Q^2;
LAC = TC/Q = 240 - 10Q + 5Q^2;
240 - 20Q + 15Q^2 = TC/Q = 240 - 10Q + 5Q^2
15Q^2 - 5*Q^2 = -10Q + 20*Q;
10Q^2 = 10Q;
10Q*(Q - 1) = 0; Q = 1.
P = LMC = 240 - 20*1 + 15*(1^2) = 235
где, * - умножить, ^ - степень
|
Всего сообщений: 1 | Присоединился: декабрь 2011 | Отправлено: 18 дек. 2011 0:51 | IP
|
|
Juliette


Новичок
|
     
помогите,пожалуйста, решить задачу!
в стране А трудозатраты на производство 1 т пшеницы составляют 400 ч.ч.
(человекчасов), а в стране В-500 ч.ч. В стране А трудозатраты на производство 1т риса составляют 500ч.ч.,а в страане В-600ч.ч. При какой пропорции обмен между странами А и В оказался бы взаимовыгодным?
|
Всего сообщений: 5 | Присоединился: декабрь 2011 | Отправлено: 18 дек. 2011 19:08 | IP
|
|
Shkolnik


Новичок
|
     
ПОЖАЛУЙСТА ПОМОГИТЕ РЕШИТЬ !!!
1) Издержки фирмы заданы функцией TC=0,5Q²+Q+6, а цена на её продукцию не зависит от объёма выпуска и равна 100 ден. ед. Определите выпуск, при котором прибыль фирмы максимальна и величину этой прибыли. По возможности описать ход решения.
2) На рынке совершённой конкуренции рыночный спрос задан функцией Q=50-P, а предложение выражается функцией Q=-10+2P. Функция общих издержек каждой фирмы, работающей на этом рынке, задаётся TC=5Q²+10Q.
Определите: а) объём производства одной фирмы, при котором её прибыль максимальна и величину этой прибыли.
б) Количество фирм на рынке.
Государство установило максимальный уровень цены, равный 15 ден. ед.
в) объём производства одной фирмы, при котором её прибыль максимальна и величину этой прибыли при новой цене.
г) как измениться количество фирм на рынке? По возможности описать ход решения.
3) Сельскохозяйственная фирма, действующая на рынке совершенной конкеренции, максимизирует прибыль, выращивая 12 тонн кукурузы в год. Определите рыночную цену тонны кукурузы, если функция издержек фирмы имеет вид TC=2Q²+3Q. По возможности описать ход решения.
|
Всего сообщений: 13 | Присоединился: декабрь 2011 | Отправлено: 18 дек. 2011 21:26 | IP
|
|
Sokratus


Долгожитель
|
      
Цитата: Skyrazor написал 18 дек. 2011 2:51
I. Фирма действует на конкурентном рынке. Функция общих издержек производства имеет вид TC = 100 + Q^2; MC = 2Q; FC = 100 дол.
1) Если цена единицы товара равна 60 дол., то сколько нужно произвести товаров, чтобы максимизировать прибыль?
2) Чему равен объём этой прибыли?
3) Каков минимальный уровень рыночной цены, до которого фирма будет продолжать производство?
II. Функция общих издержек конкурентной фирмы в долгосрочном периоде имеет вид TC = 2400Q - 10Q + 5Q^3. Определите уровень равновесной цены продукта фирмы в долгосрочном периоде.
I. 1) P = MC; 60 = 2Q; Qc = 30;
2) П = TR - TC = PQ - TC = 60*30 - (100 + 30^2) = 800 долл.;
3) P = AVCmin; VC = TC - FC = 100 + Q^2 - 100 = Q^2; AVC = VC/Q = Q^2/Q = Q. Очевидно, что AVC минимальны и равны 0 при нулевом объеме выпуска. Следовательно, фирма прекратит производство при P = 0.
P.S.: У Вас точно нет ошибки в записи функции издержек?
II. P = LATCmin. ATC = TC/Q = (2400Q - 10Q^2 + 5Q^3)/Q = 2400 - 10Q + 5Q^2. ATCmin находим, как первую производную функции ATC, приравненную к нулю: (2400 - 10Q + 5Q^2)` = 0; -10 + 10Q = 0; 10Q = 10; Qс = 1. P = ATCmin = 2400 - 10*1 + 5*1^2 = 2395.
|
Всего сообщений: 599 | Присоединился: декабрь 2008 | Отправлено: 18 дек. 2011 23:52 | IP
|
|
turbolit


Новичок
|
      
Помогите решить до етой ссылке внешняя ссылка удалена
|
Всего сообщений: 1 | Присоединился: декабрь 2011 | Отправлено: 19 дек. 2011 0:25 | IP
|
|
|

 Форум
Форум

 Экономика
Экономика

 Микроэкономика
Микроэкономика

 Форум
Форум

 Экономика
Экономика

 Микроэкономика
Микроэкономика